3.4. Функция Лагранжа. Условия оптимальности

Рассмотрим m-мерный вектор

Определение. Функцию

где x∈Г, y≥0, называют функцией Лагранжа для основной задачи выпуклого программирования.

В задачах классического анализа об условном экстремуме важную роль играет метод множителей Лагранжа: решение исходной задачи ищется среди стационарных точек функции L(x,y).

В задачах выпуклого (и, в частности, линейного) программирования функции Лагранжа также отводится важное место: при определенных условиях задача выпуклого программирования сводится к отысканию седловой точки функции Лагранжа.

Определение. Пара х*, у* называется седловой точкой функции L(x,y) на множестве x∈ Г, y≥0,

если

и

для всех х∈Г, y≥0. Формулу (3.6) можно записать также следующим образом:

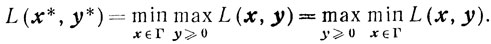(3.7)

Теорема 3.1.Если пара х*, y* - седловая точка функции Лагранжа L(x,y) на множестве х∈Γ, y≥0, то X* - оптимальная точка основной задачи выпуклого программирования (3.2).

Доказательство. Из (3.5) и (3.6) получаем

Из левого неравенства следует

а поскольку y*≥0 и это неравенство имеет место для любого y≥0, то h(х*)≤0.

В частности, (3.9) имеет место и для y = 0, то есть

а следовательно (так как y*≥0 и h(x*)≤0),

Если х∈Х, то из (3.1) и (3.4) следует, что h(x)≤0 и поэтому для х∈Х будет

Так как (3.8) имеет место для всех x∈Г и, в частности, для x∈Х, то из правого неравенства (3.8) и из (3.10) и (3.11) получаем для всех х∈Х неравенства

Но х*∈X (так как х*∈Г и h(x*)≤0) и, следовательно, х* - оптимальная точка.