3.5. Теорема Куна-Таккера

Следующей теореме отводится основная роль в математическом программировании. Теорема эта носит имя авторов.

Теорема 3.2 (Куна-Таккера).Пусть в основной задаче (3.2) выпуклого программирования

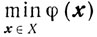
множество X = {х∈Г: f(x)≥}} обладает свойством регулярности (3.3).

Необходимым и достаточным условием оптимальности х* является существование такого y*≥0, чтобы пара х*, y* была седловой точкой функции Лагранжа L(x,y) на множестве х∈Г, y≥0.

Достаточность. Доказана в теореме 3.1.

Необходимость. Пусть х* оптимален. Рассмотрим в (m+1)-мерном пространстве Е_m+1 множества

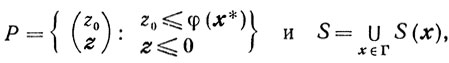
где S(x) определяется для каждого x∈Г следующим образом:

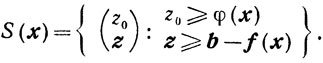
Покажем, что множества Р и S выпуклы. Выпуклость множества Р очевидна. Пусть

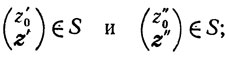
покажем, что и

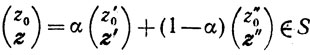
для всех α∈[0, 1]. Так как 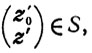, то найдется х'∈Т такой, что

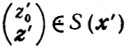
и аналогично

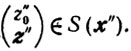
Нам достаточно показать, что

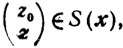
где x = αx + (1-α)x". Из выпуклости φ(x) и -φ(x) следует

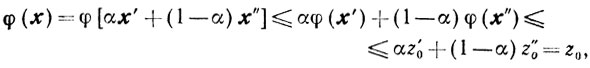
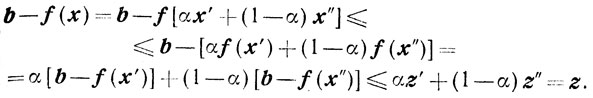
Таким образом,

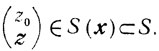
Теперь докажем, что множества Р₀ и S не имеют общих точек. Здесь

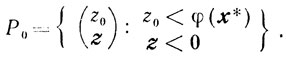
Для каждого ч∈Х ввиду оптимальности х* будет

z₀≥φ(x)≥φ(x*), но в Р₀ z₀<φ(x*).

Для каждого х∈Г такого, что х∈Х, найдется хотя бы один номер i такой, что

z_i≥b_i-f_i(x)>0, но в Р₀ z_i<0.

Итак, множества S и Р₀ выпуклы и не имеют общих точек. В соответствий с теоремой 2.5 существует гиперплоскость, разделяющая эти множества, то есть существует вектор

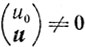(3.12)

такой, что

(3.13)

для всех

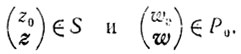
Поскольку множеству Р₀ принадлежат точки со сколь угодно большими по модулю отрицательными компонентами, то необходимо должно быть

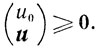(3.14)

Неравенство (3.13) остается справедливым и тогда, когда 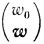принадлежит границе Р; поэтому, выбрав

получим для всех x∈Γ

Убедимся теперь, что u₀>0. Предположим, что u₀ = 0. Тогда (3.15) примет вид

≥0 для всех x∈Γ.

Так как u≥0 (см. (3.14)), и u≠0 (см. (3.12)), а для всех х∈X будет

b - f(x) ≤ 0,

то при u_i > 0 равенство

b_i - f_i(x) = 0

будет выполняться для всех х∈Х, что противоречит свойству регулярности (3.3).

Значит, из предположения u₀ = 0 вытекает u = 0, что противоречит (3.12). Итак, u₀ > 0.

Пусть

y^* = ¹/_u0u≥0,

тогда (3.15) примет вид

φ(x^*)≤φ(x) + ^*, b - f(x)>

для всех x∈Γ, а для х = х^* отсюда вытекает

^*, b - f(x^*)>≥0(3.16)

Но y^*≥0, а

b - f(x^*)≤0

(так как х^*∈X); поэтому

^*, b - f(x^*)> = 0(3.17)

Для любого y ≥ 0 будет

^*)>Ͱ0(3.18)

Из (3.16), (3.17) и (3.18) получаем

φ(x^*) + ^*)>≤φ(x^*) + ^*, b - f(x^*)>≤φ(x) +

для всех x∈Γ, y≥0 или

L(х^*, y)≤L(х^*, y^*)≤L(х, y^*), х∈Γ, y≥0.

Замечание. Условия регулярности (3.3) в формулировке теоремы можно ослабить, однако полностью избежать некоторых условий регулярности для нелинейных ограничений нельзя, что видно хотя бы из следующего простого примера.

Пусть в E₁ заданы

φ(x) = -x, f(x) = -x², b = 0, Г = {x: x≥0}.

Таким образом, задача выпуклого программирования имеет вид

min(-х)

при условиях

-х²≥0, х≥0.

[ля множества X, состоящего здесь из одной точки x = 0, не выполняются условия Слейтера. Очевидно, что x^* = 0 и φ(x^*) = 0, но функция Лагранжа

L(x, y) = - х + yx²

при х≥0 и y≥0 вообще не имеет седловой точки.

Замечание. Если множество X определяется только линейными неравенствами, то теорема 3.2 верна без каких бы то ни было дополнительных условий на X. Соответствующая теорема будет доказана несколько позже.