4.4. Геометрическая интерпретация основной задачи линейного программирования

В пространстве Е_n множество R₁ можно рассматривать как пересечение полупространств (при n = 2 - полуплоскостей):

(Ax)_i≥b_i ,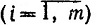

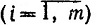x_j≥0 .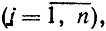

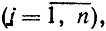Рассмотрим семейство

- семейство параллельных гиперплоскостей (при n = 2 - параллельных прямых). Вектор -с направлен в сторону убывания целевой функции. На рисунке 4.1 изображен случай, когда множество R₁ ограничено - многоугольник.

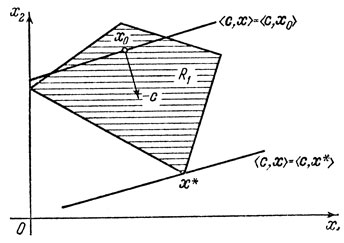
Рис. 4.1

Рассмотрим некоторую точку x₀∈R₁ Ей соответствует значение целевой функции

Теперь будем перемещать прямую

в направлении -с, то есть в направлении убывания величины λ, до тех пор, пока не придем в такую точку x^*∈R₁ для которой значение λ минимально. Геометрический смысл задачи (4.1) здесь очевиден.

Легко изобразить на чертеже, когда R₁ неограничено, но решение существует; когда решение существует, но не единственно; и, наконец, когда R₁ неограничено и <с, x> неограничена на R₁.