4.5. Основные теоремы
Сформулируем, во-первых, теорему, которая является частным случаем теоремы 3.5 (когда φ(x) линейна) и поэтому в отдельном доказательстве не нуждается.
Будем обозначать функцию Лагранжа для задачи (4.1) так:
L1(x, y) = <c, x> + <y, b - Ax>. (4.3)
Теорема 4.1. Для того чтобы точка х*∈R1 была оптимальной для основной задача линейного программирования, необходимо и достаточно существование y*≥0 такого, чтобы пара х*, y* была седловой точкой функции Лагранжа L1(x, y) в области х≥0, y≥0, то есть
L1(x*, y)≤L1(x*, y*)≤L1(x, y*). (4.4)
Замечание 1. Из соотношения (3.35) следует, что необходимым и достаточным условием оптимальности х* для задачи (4.1) является следующее представление вектора с:
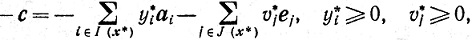 (4.5)
(4.5)где
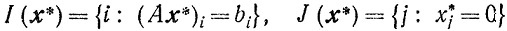
и
АТ = [а1, а2, ..., am].
Замечание 2. Из теорем 3.3 и 4.1 следует, что для х* и y* выполняются следующие равенства:
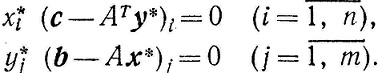 (4.6)
(4.6)Теорема 4.2 (двойственности). Прямая и двойственная задачи либо обе имеют оптимальные точки х* и y*, причем
<с, x*> = <b, y*>, (4.7)
либо обе их не имеют.
Доказательство. Рассмотрим функцию Лагранжа для задачи (4.2). Для этого запишем эту задачу в виде основной задачи линейного программирования, то есть в виде (4.1).
Ясно, что задача (4.2)
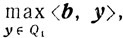
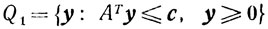
эквивалентна задаче

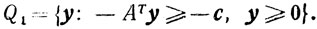
А для этой задачи, поскольку она записана в виде основной задачи, функцией Лагранжа будет
L2(y, x) = -<b, y> + <x, -c + ATy>. (4.8)
Седловой точкой для L2(y, x) в области y≥0, x≥0 будет пара y', x' такая, что
L2(y', x)≤L2(y', x')≤L2(y, x'). (4.9)
Сравнивая (4.8) и (4.3), получаем
L2(y, x) = - [<c, x> + <y, b - Ax>] = - L1(х, y). (4.10)
Из (4.10), (4.9) и (4.4) следует, что если х*, y* - седловая точка для L1(x, y), то y*, х* - седловая точка для L2(y, x), а значит, либо x* и y* оптимальны соответственно для задач (4.1) и (4.2), либо, когда седловая точка отсутствует, то и задача (4.1), и задача (4.2) не имеют решений.
Наконец, равенство (4.7) следует из формул (4.6).
Теорема 4.3. Для любых допустимых x∈R1 и y∈Q1 выполняется неравенство
<c, x> ≥ <b, y>. (4.11)
Доказательство. Из неравенств, определяющих R1 и Q1, следует
<c, x> ≥ <ATy, x> = <y, Ax> ≥<y, b> = <b, y>
Теорема 4.4. Если x*∈R1 и y*∈Q1, а
<c, x*> = <b, y*>.
то x* и y* оптимальны соответственно для задан (4.1) и (4.2), и обратно.
Доказательство. Для любого x∈R1 в силу (4.11) и условия теоремы будет
<c, x> ≥ <b, y*> = <c, x*>.
то есть х* оптимален. Аналогично доказывается оптимальность y*. Обратное утверждение теоремы содержится в теореме двойственности 4.2.
Теорема 4.5. Если линейная функция <c, x>, c≠0 ограничена снизу на непустом множестве R1, то существует точка x*∈R1 такая, что
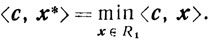
Доказательство. Во-первых, запишем неравенства, определяющие множество R1, в следующем виде:

Здесь  , где Е - единичная матрица, а dТ = (bТ, 0, 0, ..., 0).
, где Е - единичная матрица, а dТ = (bТ, 0, 0, ..., 0).
Обозначим 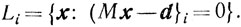 Тогда
Тогда
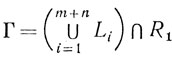
является границей множества R1, причем Γ≠0, поскольку R1 является пересечением выпуклого замкнутого множества {х: х≥0}, заведомо обладающего граничными точками, с выпуклым замкнутым множеством {х: Ах≥b}.
Не умаляя общности, можно считать, что
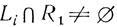
лишь для 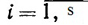 , s≤m + n, поэтому
, s≤m + n, поэтому
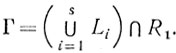
Доказательство будем вести по индукции числа n - размерности пространства Еn. Для Е1 (одномерный случай) допустимое множество R1 может быть либо точкой, либо отрезком, либо полупрямой, для которых теорема очевидна.
Предположив, что теорема справедлива для Е1, Е2,... Ek-1, докажем ее для Еk.
Так как Li∩R1⊂Ek-1 (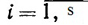 ), то по индуктивному предположению для любого
), то по индуктивному предположению для любого 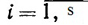 найдется xi∈Li∩R1 такой, что
найдется xi∈Li∩R1 такой, что
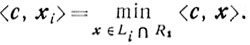
Из определения Г следует, что существует x*∈Г такой,
что
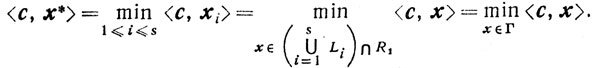
Осталось показать, что
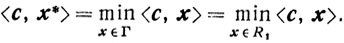
Для этого достаточно убедиться, что для любой точки х∈R1\Г существует такая граничная точка x'∈Г, что
<c, x'>≤<c, x>.
Рассмотрим точку ̄х = х - λс, λ>0. Поскольку x - внутренняя точка для R1, то ̄х = х - λс ∈ R1 по крайней мере для малых X. По предположению <с, ̄x> ограничена снизу:
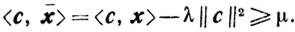
Следовательно,
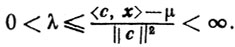
Тогда существует
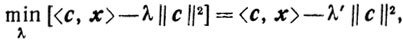 (4.12)
(4.12)где минимум берется по всем к таким, что

Ясно, что ̄х = х - λ'с ∈Г. В самом деле, если x' - внутренняя точка для R1, то найдется λ" >λ>0 такое, что х - λ"с ∈R1. Но тогда
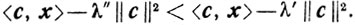
А это противоречит (4.12). Итак,
х'∈Γ и <с, x'><<c, x>.
Теорема доказана.
Замечание. Следует обратить внимание на то, что теорема справедлива, вообще говоря, лишь для задач линейного программирования.
Рассмотрим, например, следующую задачу: минимизировать х2 на множестве
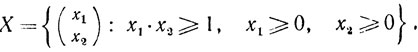
Очевидно, что X выпукло и замкнуто,
но не существует точки из X, в которой достигается infX x2 (рис. 4.2).
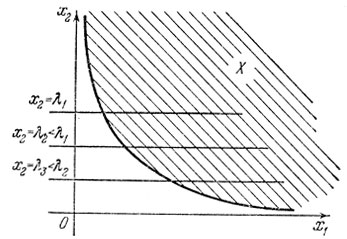
Рис. 4.2
Теорема 4.6. Для существования решения одной из двойственных задач (и, следовательно, обеих) необходимо и достаточно, чтобы
R1≠∅ и Q1≠∅.
Доказательство. Необходимость очевидна.
Достаточность. Пусть y∈Q1 тогда для любого x∈R1 имеет место (4.11):
<c, x>≥<b, y>.
а тогда по теореме 4.5 задача (4.1) имеет решение и, значит, имеет решение и задача (4.2) (ввиду теоремы 4.2).
Следствие а*. Если <c, x> (<b, y>) неограничена снизу на R1 (сверху на Q1), то
Q1 = ∅ (R1 ≠ ∅).
* (В скобках приводится двойственное утверждение.)
Следствие б. Если Q1 = ∅ (К1 = ∅), a К1 ≠ ∅ (Q1 ≠ ∅), то R1 (Q1) неограничено и <c, x> неограничена снизу на R1 (<b, y> неограничена сверху на Q1).
Теорема 4.7. Если
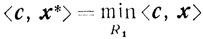
и если существуют х1, х2, ..., хM такие, что
(а)
xi∈R1 (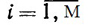 ),
),
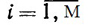 ),
),(б)
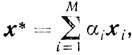
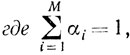
(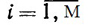 ), то
), то
<c, x*> = <c, x1> = ... = <c, xM>.
Доказательство. Предположим, что
<c, x*> ≤ <c, x1> ≤ ... ≤ <c, xM>.(4.13)
Тогда
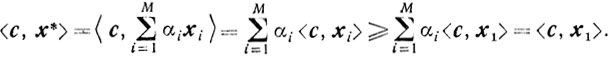
Учитывая (4.13), получаем
<c, x*> = <c, x1>.
Сделаем индуктивное предположение:
<c, x*> = <c, x1> = ... = <c, xk> (k<M).
и докажем, что
<c, x*> = <c, xk+1>.
Действительно,

Отсюда
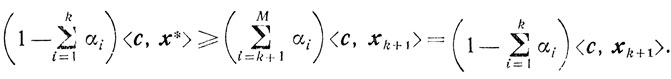
И так как 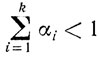 (поскольку k<М), то
(поскольку k<М), то
<c, x*> ≥ <c, xk+1>.
А тогда (см. (4.13))
<c, x*> = <c, xk+1>.
Теорема 4.8. Если задача (4.1) имеет решение х*, то существует угловая точка х такая, что
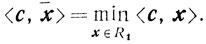
Доказательство. 1) Если R1 ограничено, то из теоремы 2.6 следует, что существуют такие угловые точки х1, х2, ..., xN множества R1, что для любого x∈R1 и, в частности, для х* будет
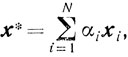
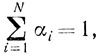
αi≥0 (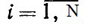 )
)
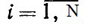 )
)Вычеркнем из системы точек х1, х2, ..., xN те, которым соответствуют αi = 0. Не ограничивая общности, можем полагать, что это точки хM+1, хM+2, ..., xN. Тогда
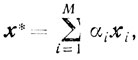
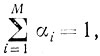
αi>0 (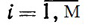 )
)
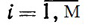 )
)то есть выполняются условия теоремы 4.7, откуда и следует утверждение теоремы
2) Пусть R1 неограничено, а x* оптимален. Очевидно, что для достаточно большого числа μ>0 множество
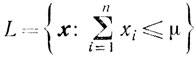
таково, что
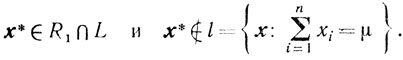
Так как пересечение "ортанта" x≥0 с множеством L ограничено, то и R1∩L ограничено и, следовательно (теорема 2.6), существуют угловые точки x1, x2, ..., хM множества R1∩L такие, что
<c, x*> = <c, x1> = ... = <c, xM>.
Если хотя бы одна точка xi∉l, то теорема доказана, поскольку тогда хi будет угловой точкой множества R1. Если все xi∈l (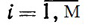 ), то из представления
), то из представления

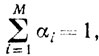
αi>0 (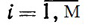 )
)
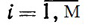 )
)следует x*∈l, что противоречит выбору числа μ>0 при построении множества L.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'