4.6. Алгебраическая характеристика угловой точки
Ранее было введено геометрическое определение угловой точки. Однако для того, чтобы уметь находить (вычислять) угловую точку, необходима ее алгебраическая характеристика.
Пусть, как и прежде,
I(x) = {i: (Ax)i = bi}, J(x) = {j: xj = 0}, J = {j = 1, 2, ..., n}.
Система уравнений
(Az)i = bi i∈I(x),
zj = 0 j∈J(x)(4.14)
будет квадратной, если
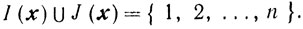
Не умаляя общности, можно полагать
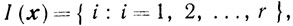
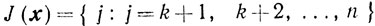
и тогда при r = k система уравнений (4.14) будет квадратной.
Теорема 4.9. Для того чтобы точка х≠0 являлась угловой точкой множества R1, необходимо и достаточно, чтобы х удовлетворял неособенной квадратной системе уравнений (4.14).
Достаточность. Пусть x∈R1 и существует матрица
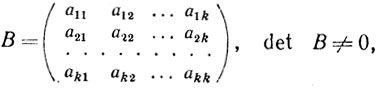 (4.15)
(4.15)такая, что
B̄x = ̄b.(4.16)
Здесь
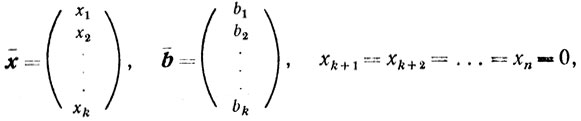
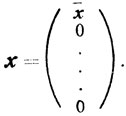 (4.17)
(4.17)Предположим, что х - не угловая точка, то есть существуют x'∈R1, x"∈R1 и х'≠x"≠x такие, что
x = αx' + (1 - α)x", α∈(0, 1).
Для j>k
xj = αx'j + (1 - α)x"j = 0.
И так как α>0, (1-α)>0, x'i≥0, x'j≥0, то
x'i = x'j = 0 (i = k + 1,..., n).
Далее,
Вх̄'≥b̄, Вх̄"≥b̄, αВх̄'+(1 - α,)Bx̄"=b̄
поэтому
Вх̄' = Вх̄" = b̄ ,
и поскольку detB≠0, то х̄'=х̄", следовательно, x'=x", что противоречит предположению.
Необходимость. Пусть х - угловая точка множества R1.
1) Покажем, что хотя бы для одного i будет
(Ax)i = b
Предположим, что такого номера i не существует. Так как x≠0, то найдется такое j, что xj > 0. Рассмотрим
(x')T = (x1, x2,....,xj-1, xj+ε, xj+1,...,xn)≥0
и
(x")T = (x1, x2,....,xj-1, xj+ε, xj+1,...,xn)≥0
Из предположения, что Ax>b, следует для достаточно малого ε
Ax'≥b, Ax"≥b,
то есть х'∈R1, x"∈R1. Но
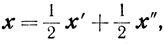
что противоречит предположению (точка х по предположению угловая). _______
2) Пусть (Ax)i = bi для i = 1,..., r и xj = 0 для j = k + 1,..., n
Обозначим
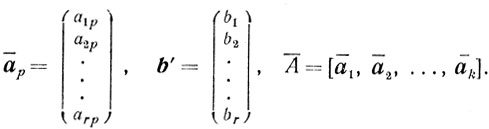
В этих обозначениях А̄х̄ = b' и х̄ > 0.
Докажем, что ā1, ā2,...,āk линейно-независимы (в этом случае k≤r).
Предположим противное, то есть, что существует х̄'≠0 такой, что А̄х̄' = 0.
Возьмем
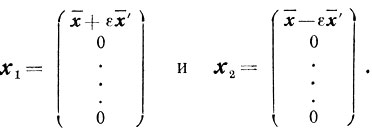
Легко видеть, что x1∈R1, x2∈R1 при малых ε. Но
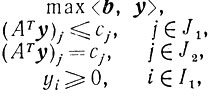
что противоречит предположению. Итак, k≤r.
Вычеркнув (r - k) строк из Ā, получим матрицу В, для которой выполняются (4.15)-(4.17).
Следствие. Число угловых точек множества R1 конечно.
Это утверждение очевидно, поскольку число не особенных квадратных клеток (подматриц) матрицы условий конечно.
Определение. Если точка хТ = (хāТ, 0, ..., 0), x̄ > 0 - угловая, то систему линейно-независимых векторов а̄1, а̄2, ..., а̄kв представлении
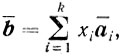
xi > 0 (j = 1,...., k)
называют базисом угловой точки, а матрицу
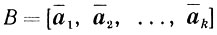
матрицей базиса угловой точки.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'