5.3. Методы отыскания исходной угловой точки

Наиболее распространенными являются так называние методы искусственного базиса, суть которых состоит следующем: строится такая вспомогательная каноническая задача линейного программирования с заранее известной угловой точкой, по решению которой тривиально строится либо угловая точка, либо оптимальная точка задачи (5.1). Таким образом, процесс отыскания исходной угловой точки связан с решением новой задачи линейного программирования и поэтому он, вообще говоря, столь же трудоемок, как и процесс отыскания решения задачи (5.1) при известной исходной угловой точке.

Метод искусственного базиса. Рассматривается задача отыскания угловой точки множества

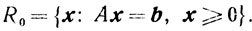
Не умаляя общности, можно предполагать, что b≥0. Построим следующую вспомогательную задачу в пространстве Е_n+m:

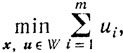
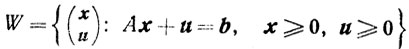(5.12)

с заранее известной угловой точкой

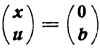
множества W. Применяя симплексный метод, находят (^x*_u^*) - решение задачи (5.12). Обозначим

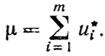
Теорема 5.1.Если μ = 0, то х^* - угловая точка множества R₀. Если μ > 0, то R₀=∅.

Доказательство. Во-первых, ясно, что задача (5.12) разрешима, поскольку W ≠ ∅ а целевая функция

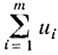
ограничена снизу нулем. Если μ = 0, то

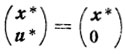
- оптимальная угловая точка задачи (5.12), поскольку эта задача решается симплексным методом, который осуществляет перебор угловых точек. Очевидно, что х^* - угловая точка множества R₀. Пусть теперь μ > 0. Предположим, что R₀≠∅, то есть найдется x∈R₀. Но тогда

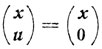
будет решением задачи (5.12), что противоречит предположению о положительности величины μ.

Заметим, что метод искусственного базиса является составной частью большинства стандартных программ для ЭВМ симплексного метода решения задач линейного программирования.

Применение метода искусственного базиса приводит к тому, что задачу (5.1) приходится решать в два этапа: сперва решать вспомогательную задачу (5.12), а затем собственно задачу (5.1). Следующий метод позволяет объединить оба этапа.

М - метод. Рассмотрим следующую вспомогательную задачу:

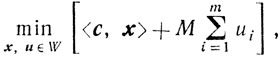
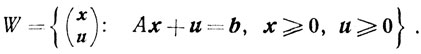(5.13)

Теорема 5.2.Если разрешима задача (5.1), то найдется такое число М₀, что для всех М ≥ М₀ в любом решении (^x*_u^*) задачи (5.13) точка х^* будет оптимальной для задачи (5.1).

Доказательство этой теоремы по сути дела является частным вариантом доказательства теоремы 10.9 о сходимости M-метода для задачи выпуклого программирования. Первую часть этого доказательства мы здесь воспроизведем.

По условию задача (5.1) разрешима, то есть существует оптимальная точка х^*. Но тогда разрешима и двойственная задача

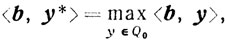
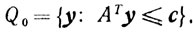
По теореме 4.4 х^* и y^* будут удовлетворять следующей системе:

Поскольку задача

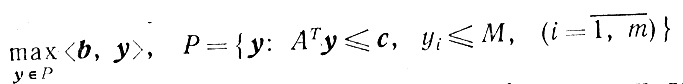
является двойственной к (5.13), то необходимым и достаточным условием существования решения задачи (5.13) (а следовательно, и двойственной к ней) будет существование решения системы неравенств

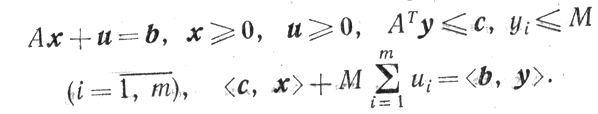(5.15)

Поскольку х^* и y^* удовлетворяют системе (5.14), то х = х^*, u = u^* = 0, y = y^* будут удовлетворять системе (5.15) для всех

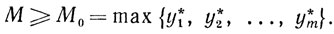
Доказательство того, что при М≥М₀ в любом решении x^*, u^* задачи (5.13) будет u^*=0 и, следовательно, x^* является решением задачи (5.1), читатель найдет в теореме 10.9.

Обсуждение. Очевидно, что при b≥0 точка

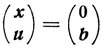
является угловой точкой множества W. Именно эту точку и выбирают в качестве исходной для применения симплексного алгоритма.

На практике нет нужды определять число М₀. В качестве М обычно выбирают достаточно большое число,

например

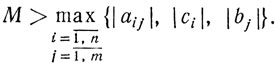
Наконец, заметим, что если М-задача (5.13) имеет решение, то существует решение системы неравенств (5.15), а следовательно, Q_o≠∅. Ввиду этого из теоремы 4.6

получаем, что если R₀≠∅ и существует решение М-задачи, то существует решение исходной задачи (5.1). Поэтому теорема 5.2 справедлива в условиях существования решения M-задачи и не пустоты множества R₀. Отсюда приходим к следующему выводу: если существуют сколь угодно большие значения М такие, что в решении (^x*_u^*) задачи (5.13) будет

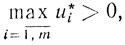
то исходная задача (5.1) неразрешима.