5.4. Вырожденность. Метод возмущений
В случае, когда угловая точка х множества R0 вырождена, число ее положительных компонент будет меньшим m. Тогда может оказаться, что λ0 = 0 (см. (5.7)) и, следовательно, при переходе в симплексном методе от вырожденной угловой точки х к Следующей угловой точке значение целевой функции может не убывать (см. (5.10)). Кроме того, как мы видели, вырожденность может повлечь за собой неоднозначность выбора вектора, исключаемого из базиса, при переходе от угловой точки х к вырожденной угловой точке xk=xk(λ0).
Эти обстоятельства теоретически могут привести к явлению зацикливания, когда через некоторое число итераций процедура симплексного метода приводит к прежней угловой точке. Для преодоления явления зацикливания существует правило выбора вектора, исключаемого из Зазиса, основанное на так называемом методе возмущений.
Предположим, угловой точке х множества R0 соответствует такая линейно-независимая система m векторов а1, a2 ,..., аm, что xB=B-1b≥0 (в отличие от не вырожденного случая, когда хв > 0), где В = [а1, а2, ...., аm].
Рассмотрим "возмущенный" вектор
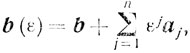
где ε - достаточно малое положительное число (ε > 0), а εj означает j-ю степень числа ε. Обозначив, как и прежде, zij, = (В-1аj)i, получаем
Так как
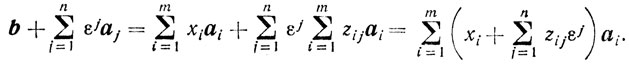
то
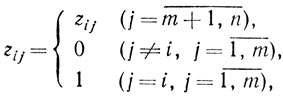 (5.16)
(5.16)Рассмотрим наряду с задачей (5.1):
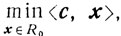
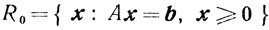
- так называемую ε-задачу:
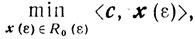 (5.17)
(5.17)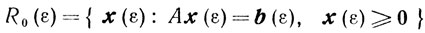
и покажем, что для всех достаточно малых ε >> 0 эта задача не вырождена.
Пусть а1, а2,... , аm-произвольная линейно-независимая система векторов матрицы А. Так как функции xi(ε) (i = 1,...,m) представляют собой многочлены относительно ε, не равные тождественно нулю (см. (5.16)), то каждый из них имеет не более n корней и, следовательно, не более n положительных корней.
Пусть η есть наименьший положительный корень среди всех положительных корней m многочленов xi(ε) (i = 1,...,m) (если положительных корней нет ни у одного из этих многочленов, то полагаем η = ∞). Величина η определяется выбранной системой линейно-независимых векторов a1, а2,... , аm, и поскольку число линейно-независимых систем векторов матрицы А конечно, то конечно и число соответствующих наименьших положительных корней η.
Пусть ε0 > 0-наименьшее из всех чисел η (то есть наименьший положительный корень всех многочленов xi(ε), построенных по всевозможным линейно-независимым системам векторов матрицы А). Ясно, что при ε<ε0 ни один из многочленов вида (5.16) не обращается в нуль (ε > 0), а следовательно, всякая угловая точка ε-задачи содержит m положительных компонент, то есть не вырождена.
Можно доказать, что для малых ε угловым точкам x ∈ R0 и х(ε) ∈ Rn (ε) соответствует один и тот же базис*, поэтому для однозначного выбора индекса s ∈ Ik, на котором достигается минимум отношения
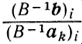
(см. (5.7))
при симплексной процедуре решения задачи (5.1), целесообразно обратиться к ε-задаче. То есть в качестве номера s вектора as, исключаемого из базиса, следует выбрать тот номер (единственный ввиду не вырожденности ε-задачи), для которого достигается минимум отношения
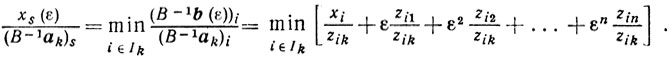
На практике нет нужды переходить к ε-задаче. Из предыдущей формулы ясно, что выбор номера s можно осуществить следующим путем.
Обозначим через Ik0(sk) совокупность индексов sk∈Ik, для которых достигается минимум отношения
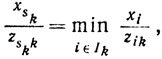
sk∈Ik0(sk)
* (Строгое обоснование этого утверждения можно найти в [14]. )
Если Ik0(sk) состоит более чем из одного элемента, то вычисляют
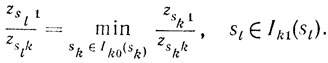
Если Ik1(sl) состоит из одного элемента, то sl и есть искомый номер. Если Ikl(sl) содержит два и более элементов, то вычисляют
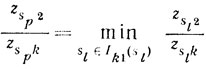
и т. д. Ясно, что такой процесс конечен и приводит к однозначному выбору искомого номера.
Опыт применения симплексного метода показал, что для исключения возможности зацикливания достаточно выбрать любой регулярный способ однозначного выбора номера s, например, в качестве s можно выбрать первый (в порядке установленной нумерации) номер, для которого достигается минимум отношения (5.7). При этом естественно, что номер k также должен выбираться (если он не единствен) регулярным способом, например, среди всех k таких, что Δk > 0 и (B-1ak)i > 0 можно выбирать тот, для которого величина Δk наименьшая.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'