5.6. О модифицированном симплексном методе

(Установившегося названия метода нет. Иногда его называют "методом обратной матрицы", иногда "вторым алгоритмом симплексного метода". )

В обычном симплексном методе на каждой итерации все элементы матрицы А преобразуются по формулам (5.11). В модифицированном методе на каждом шаге вычисляют матрицу В^-1 и затем, пользуясь ей, вычисляют

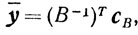
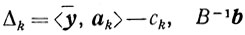
и т. д. После этого, пользуясь простыми рекуррентными формулами, переходят от матрицы

к матрице

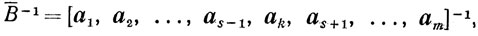
соответствующей новой угловой точке.

Таким образом, на одной итерации преобразуются и хранятся в памяти ЭВМ лишь элементы матрицы В^-1. При этом объем текущей информации, запоминаемой машиной, как правило, сокращается. Кроме того, если матрица А содержит большое число нулевых элементов, то в модифицированном симплексном методе вычислительная схема может быть составлена так, чтобы в вычислениях на каждом шаге скалярных произведений участвовали лишь ненулевые элементы матрицы А. Это существенно сокращает объем вычислений и позволяет

компактно разместить ненулевые элементы матрицы А в запоминающем устройстве машины.

Рекуррентные соотношения модифицированного симплексного метода можно получить из формул перехода от матрицы В^-1 к матрице В̄^-1.

Обозначим элементы матрицы В^-1 через a^-1_ij, а матрицы В̄^-1- через ā^-1_ij:

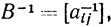
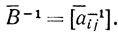
Тогда

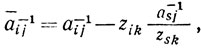
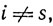
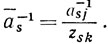
Справедливость этих формул проверяется умножением матрицы В̄ на матрицу В̄^-1, в результате которого получается единичная матрица.