5.7. Мультипликативное представление обратной матрицы

Для уменьшения количества информации, подлежащей запоминанию, в модифицированном симплексном методе часто пользуются следующим мультипликативным представлением обратной матрицы.

Назовем элементарной матрицу вида

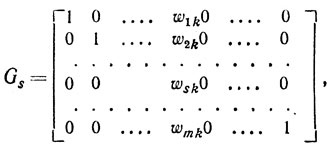
где

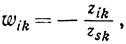
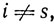
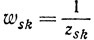
(индекс s означает, что столбец элементов w_jk стоит на s-м месте). Легко проверить, что

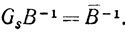
Процедура модифицированного симплексного метода начинается, как правило, с единичного базиса, которому соответствует единичная матрица G. Пусть на первом шаге в базис вместо e_s1 вводится вектор a_k1. Тогда матрицей В^-1₁, обратной к матрице нового базиса, будет

а на р-м шаге

Поскольку каждая матрица G_s определяется (m+1) числом величин s, w_1k, w_2k, ..., w_mk, то мультипликативная форма записи обратной матрицы меньше загружает память машины, чем обычная.

Замечание. Тщательный разбор алгоритма модифицированного симплексного метода, а также мультипликативной записи обратной матрицы читатель найдет в книге [14].