5.8. Двойственный симплексный метод

(Наряду с названием "двойственный симплексный метод" принято название "метод последовательного уточнения оценок", смысл которого будет выяснен в п. 5.9.)

Как мы видели, симплексный метод позволяет наряду с получением решения прямой задачи получать и решение

двойственной задачи (случай" I симплексного метода). Этот результат и лежит в основе двойственного симплексного метода решения задачи (5.1).

Суть метода состоит в таком последовательном переборе угловых точек допустимого множества Q_u двойственной задачи (5.6), при котором значение целевой функции <b, y> возрастает, то есть в применении симплексного метода к решению двойственной задачи. Поскольку двойственный симплексный метод нас интересует, как метод решения задачи (5.1), выясним, что означают для задачи (5.1) преобразования каждого итерационного шага симплексного метода, примененного к задаче (5.6).

Будем предполагать, что задача (5.6) не вырождена, то есть каждой угловой точке множества Q₀ соответствует квадратная не особенная (невырожденная) система уравнений размерности m, матрицу которой называют двойственным базисом прямой задачи (5.1).

Пусть известна угловая точка y множества Q₀. Это означает, что известен двойственный базис

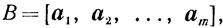
что точка y = (В^-1)^Тс_В удовлетворяет неравенству

и что

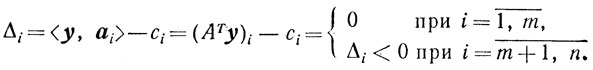
Обозначим, как и прежде,

и, кроме того,

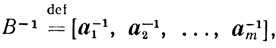
то есть через a^-1_i обозначен j-й столбец матрицы B^-1.

Рассмотрим векторы

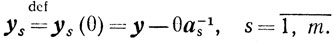
Поскольку

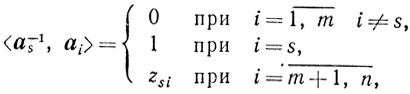
то

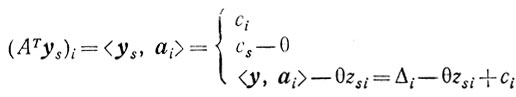(5.18)

В зависимости от знаков величин x_j и z_ij возникают три случая.

I. Если x_B≥0, то

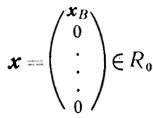
и, следовательно, точка х - оптимальная (см. случай I симплексного метода).

II. Если найдется номер s≤m такой, что x_s<0 и z_si≥0 для всех i = m+1,...,n, то y_s∈Q₀ для любого θ > 0 и, следовательно, множество Q₀ не ограничено и

при θ→+∞, то есть множество R₀ пусто (следствие из теоремы 4.6).

III. Пусть найдутся такие s≤m и i≥m+1, что x_s < 0 и z_si < 0. В этом случае делается итерационный шаг. Обозначим I_s = {i: z_si < 0 } и выберем

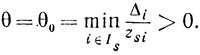
Пусть

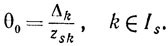(5.19)

Номер k, для которого достигается этот минимум, единствен ввиду не вырожденности задачи (5.6)^*. Покажем, что

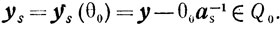
Действительно, из (5.18) и (5.19) следует

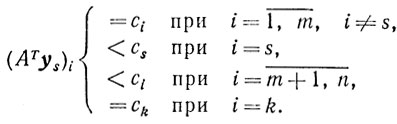
^* (Доказательство этого утверждения аналогично доказательству подобного утверждения в "случае III" симплексного метода.)

Наконец,

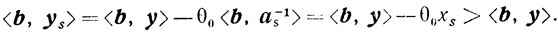
Таким образом, при переходе от точки y к точке y значение целевой функции задачи (5.6) возрастает.

Итак, итерационный шаг двойственного симплексного метода состоит в том, что из двойственного базиса выводится вектор a_s и вводится на его место а_k при этом значение целевой функции возрастает. Осталось доказать, что новая система векторов а₁, a₂, ..., a_s-1, a_k, a_s+1 ,..., a_m линейно-независима, то есть образует новый двойственный базис. Читатель в этом без труда убедится, если проведет рассуждения, аналогичные тем, которые имели место в "случае III" симплексного метода.

Поскольку число угловых точек множества Q₀ конечно, и при каждой итерации (при переходе от одной угловой точки к другой) значение целевой функции возрастает, то за конечное число итераций метод приведет к решению y^* двойственной задачи, а значит, и к решению х^* прямой задачи.

Рекуррентные соотношения алгоритма двойственного симплексного метода нетрудно получить из формул перехода от матрицы В^-1 к матрице В̄^-1 (см. п. 5.6).

Если задача вырождена, то так же, как и в случае простого симплексного метода, для двойственного метода на основе метода возмущений выработаны правила однозначного выбора номера k для величины 90, то есть правила выбора вектора, вводимого в двойственный базис.