5.9. Решение двойственной задачи как оценки влияния

Покажем, что при некоторых изменениях компонент вектора ограничений b в задаче (5.1) компоненты решения двойственной задачи (5.6) могут быть интерпретированы, как оценки влияния этих изменений на величину минимума целевой функции задачи (5.1).

Рассмотрим задачу

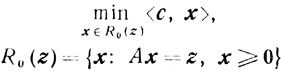(5.20)

и двойственную к ней:

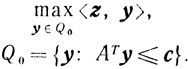(5.21)

В предположении, что задача (5.20) разрешима при некотором z, обозначим

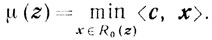
Пусть при z = z^* существует решение х^* задачи (5 20) и, следовательно, существует y^* - решение задачи (5 21)

Теорема 5.3. Если задача (5.20) не вырождена, то существует такая окрестность U (z^*) точки z^*, что для всех z ∈ U (z^*) будет

Доказательство. Так как при z = z^* задача (5.20) разрешима, то, согласно теореме 4.8, существует оптимальная угловая точка х^*. Пусть х^* имеет вид

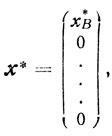
где

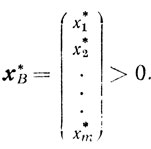
Ей соответствует базис В = [а₁, а₂, ..., а_m], detB≠0,

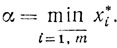
Выберем следующую окрестность:

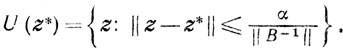
Покажем, что точка

где X_B = B^-1z будет оптимальной для задачи (5.20) при любом z ∈ U (z^*). Действительно,

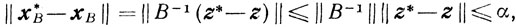
где норма выбрана следующим образом:

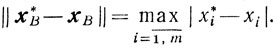
Получаем, что

то есть

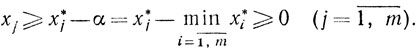
Таким образом, x≥0. И, кроме того, по построению, Ax=z, то есть x∈R₀(z).

Докажем, что х оптимален для задачи (5.20). Из условий (4.6) следует, что каждому х^*_i > 0 (i = 1,...,m) соответствует

Тогда

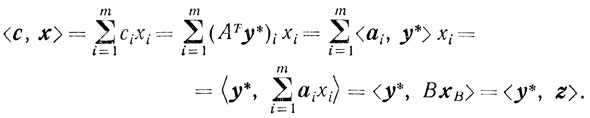
И так как x∈R₀(z), a ,y^*∈Q₀ из теоремы 4.4 вытекает оптимальность точек х и y^* и

Теорема доказана. Очевидно, что

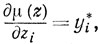
поэтому увеличение z_i приводит к увеличению или уменьшению величины μ(z) в зависимости от знака y^*_i. При этом скорость изменения μ(z) определяется величиной |y^*_i|.

Двойственный симплексный метод называют также методом последовательного уточнения оценок, поскольку угловые точки задачи (5.6), возникающие при итерациях можно рассматривать, как приближенные значения точной оценки y^*, то есть как приближенные оценки влияния условий задачи (5.1) на величину минимума целевой функции.