5.10. О применении двойственного симплексного метода к задачам с возрастающим количеством условий

Пусть найдены оптимальные угловые точки х^* и y^* задач (5.1) и (5.6) соответственно. Предположим, что к системе условий, определяющих допустимое множество R₀, добавлено еще одно неравенство

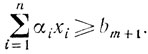
Если

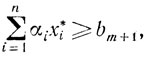
то х^* будет оптимальным и для новой задачи, поскольку добавление условий может только увеличить величину минимума целевой функции. В случае

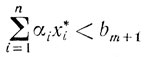
выясним, как, зная оптимальные угловые точки x^* и y^*, получить решение новой задачи.

Запишем новую задачу в каноническом виде, введя дополнительную переменную х_n+1. Обозначим

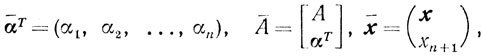
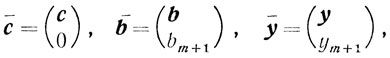
e_m+1 - (m+1)-й единичный координатный вектор. Новая задача примет вид

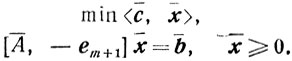(5.22)

Согласно правилам (4.18)-(4.19) двойственной к (5.22) будет задача

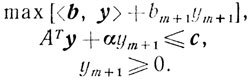(5.23)

Так как точка y^*- угловая для задачи (5.6), то

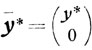
будет угловой точкой для задачи (5.23), поскольку из линейной независимости системы векторов a₁, а₂, ... ..., а_m-базиса угловой точки y^* - следует линейная независимость системы векторов

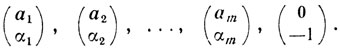
Теперь естественно, принимая y^* за исходную угловую точку, решать задачу (5.22) двойственным симплексным методом. Как правило, для получения решения задачи (5.22) требуется небольшое число итераций.

Очевидно, что все, сказанное в этом пункте, остается в силе, если к неравенствам, определяющим множество R₀, добавляется не одно, а несколько новых.