5.11. Метод одновременного решения прямой и двойственной задач

(Этот метод часто называют методом последовательного сокращения невязок. )

Рассмотренные выше методы состояли из двух этапов. На первом этапе требовалось определить угловую точку допустимого множества, после чего на втором этапе, исходя из найденной угловой точки, строился процесс отыскания оптимальной точки. Оба этих этапа, вообще говоря, одинаково трудоемки. Итерационный процесс метода одновременного решения прямой и двойственной задач начинается с любой допустимой (необязательно угловой) точки двойственной задачи, отыскать которую в реальных случаях часто не представляет труда. Например, если с ≥ 0, то y = 0 принадлежит множеству Q₀.

Итак, рассмотрим прямую каноническую задачу

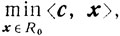
(5.1)

и двойственную к ней:

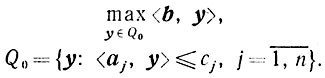(5.6)

Предположим, что известна точка y₀ ∈ Q₀. Обозначим

и рассмотрим так называемую расширенную задачу

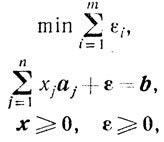
где ε^T = (ε₁, ε₂, ..., ε_m), и "укоротим" ее следующим образом:

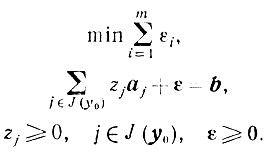(5.25)

Следующая теорема лежит в основе рассматриваемого метода.

Теорема 5.4.Если в решении z^*, ε^* задачи (5.25) ε^* = 0, то точка х^* такая, что

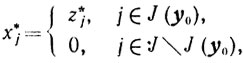
будет оптимальной для задачи (5.1), а точка y₀ будет оптимальной для задачи (5.6).

Доказательство. Очевидно, что x^*∈R₀. Из того, что точка y₀ допустима для задачи (5.6), а ε^* = 0, получаем

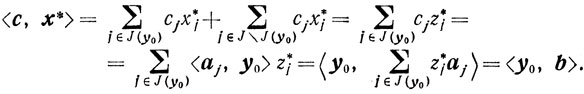
Ввиду того, что x^*∈R₀, y₀∈Q₀ и <c, x^*> = <b, y₀> на основании теоремы 4.4, следует оптимальность x^* и y₀. Теорема доказана.

Построим задачу, двойственную к (5.25):

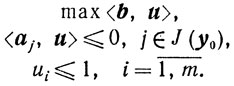(5.26)

Задачи (5.25) и (5.26) разрешимы. Действительно, так как b≥≥0, то z_j = 0, j∈J(y₀) ε=b допустимы для (5.25), а u = 0-допустимая точка для (5.26), то по теореме 4.6 обе задачи разрешимы.

Пусть u^* - решение задачи (5.26). Обозначим

и

Векторы Δ⁰ и δ^* часто называют векторами невязок.

В зависимости от характера величин ε^*_i (i=1,...,m) и δ^*_j, j∈J различают три случая.

I. Если

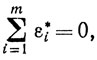
то на основании теоремы 5.4 точка х^* является решением задачи (5.1).

II. Пусть

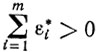
и найдется такой номер j∈J\J(y₀), для которого δ^*_j >v0. В этом случае будем строить новую точку y ∈ Q₀, которой соответствует большее значение целевой функции задачи (5.6). Выберем

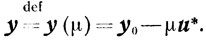
Тогда

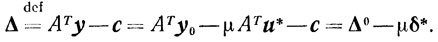(5.27)

Заметим, что

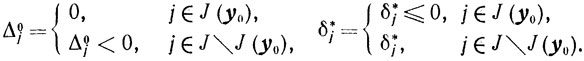(5.28)

Выбирая

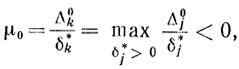(5.29)

получаем, что

а значит, ввиду (5.27) y=y(μ₀) ∈ Q₀. Поскольку z^*, e^* - решение задачи (5.25), а u^*- решение двойственной к ней задачи (5.26), то

(теорема 4.2). Вследствие этого

так как μ₀<0, а

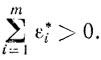
Итак, итерационный шаг метода состоит в том, что решают укороченную задачу (5.25), вычисляют величину μ₀ и строят новую точку y=y(μ₀). При этом на первом итерационном шаге в качестве исходной угловой точки задачи (5.25) выбирают точку с компонентами z_j = 0, j∈J(y₀), и ε_i = b_i≥0 (i=1,....,m) и затем применяют симплексный метод. На следующем итерационном шаге строят новую укороченную задачу

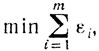
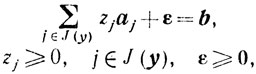(5.30)

и далее процесс повторяется. При этом в качестве исходной угловой точки задачи (5.30) выбирают точку, ненулевыми координатами которой являются положительные компоненты оптимальной угловой точки z^*, ε^* задачи (5.25), поскольку

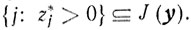
Это включение следует из того, что значениям z^*_j > 0 соответствуют значения

(из соотношения вида (4.6) в применении к решениям задач (5.25) и (5.26)) и, следовательно (см. (5.27) и (5.28)),

Но, по построению,

Что и требовалось доказать.

Процесс решения задачи (5.30) начинается с введения в базис вектора a_k (номер k выбирают из (5.29)). Заметим, что k∈J(y), поскольку Δ_k = 0 (см. (5.29)).

В результате этой процедуры величина

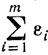
становится меньшей, чем

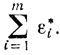
В самом деле, значения

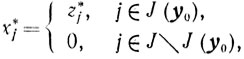
и

образуют угловую точку допустимого множества задачи (5.24). Введению а_k в базис задачи (5.30) соответствует

обычный итерационный шаг симплексного метода решения задачи (5.24) (см. (5.29)). Но при каждом итерационном шаге симплексного метода, в случае не вырожденности задачи (5.24), значение целевой функции убывает,

то есть

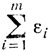
становится меньше

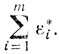
Отсюда следует, что на каждом шаге метода одновременного решения прямой и двойственной задач, то есть в результате решения новой укороченной задачи, оптимальное значение целевой функции

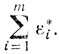
убывает по сравнению с оптимальным ее значением в предыдущей укороченной задаче. Из этого вытекает конечность метода. Заметим также, что поскольку для каждой задачи вида (5.30) имеется исходная угловая точка, а множество индексов J (y) от шага к шагу меняется незначительно, то число итераций симплексного метода решения задачи (5.30) невелико.

III. Если

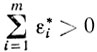
и δ^*≤0 то

для любого μ<0, так как

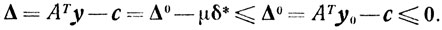
Но

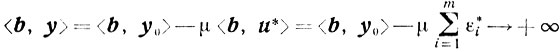
при μ→-∞, то есть <b, y> не ограничена на Q₀, a, следовательно, R₀=∅ (следствие из теоремы 4.6).

Итак, метод одновременного решения прямой и двойственной задач состоит в построении последовательности решений укороченных задач до тех пор, пока не возникнет случай I и будет найдено решение, либо-случай III, обнаруживающий, что R₀=∅.