Глава 6. Метод штрафных функций

6.1. Описание метода

Как правило, численные методы решения задач безусловной минимизации и методы решения задач математического программирования имеют качественное различие с точки зрения их трудоемкости. Так, например, вдобавок к трудностям, возникающим в методе градиентного спуска (гл. 9, п. 9.5) решения задачи отыскания безусловного минимума, в методе условного градиента (гл. 10, п. 10.1) решения задачи математического программирования на каждом итерационном шаге приходится еще решать задачу линейного программирования. В связи с этим весьма перспективными могут оказаться попытки свести задачу математического программирования к последовательности задач безусловной минимизации.

Идея метода штрафных функций состоит в следующем. Исходную задачу математического программирования

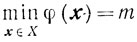(6.1)

заменяют задачей о безусловной минимизации однопара-метрического семейства функций

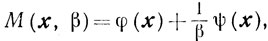
либо задачей минимизации функции М(х, β) на некотором множестве Г, более простой структуры с точки зрения численных методов минимизации, чем исходное множество X. При этом функцию ψ(х) выбирают таким

образом, чтобы решение задачи

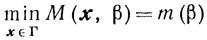(6.2)

сходилось при β→0 к решению исходной задачи либо, если это обеспечить не удается, то по крайней мере чтобы m(β)→0 при β→0.

Итак, метод штрафных функций состоит в построении функции М(х, β), в выборе последовательности {β_k} и в решении соответствующих этой последовательности задач вида (6.2).

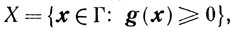
Рассмотрим следующий вид задания множества X:

где

а множество Г обладает, как об этом говорилось выше, простой структурой. Как правило, Γ = Е_n, и тогда (6.2) является задачей безусловной минимизации, либо Γ = {х: x≥0}, либо Г = {х: а≤х≤b}. В обоих последних случаях задания множества Г сложность многих численных методов решения задачи (6.2) примерно такая же, что и в случае, когда Γ = Е_n.

Определение. Непрерывную функцию

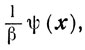
определенную для всех х ∈ Г и β > 0, будем называть штрафом, если ty(x) такова, что

Весьма широкое применение находит следующий выбор функции ψ(x):

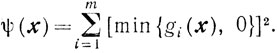(6.4)

Условия (6.3) при таком выборе функции ψ(х) с очевидностью выполняются.

Можно следующим образом наглядно проиллюстрировать метод штрафных функций. Пусть

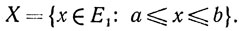
Тогда

На рис. 6.1 изображена функция 1/β ψ(x) для двух различных значений β: β₁ > β₂ > 0.

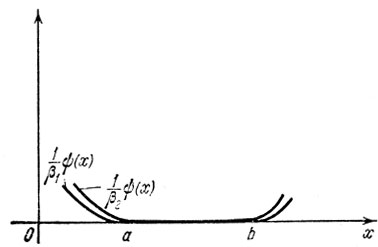
Рис. 6.1

Пусть функция φ(x) линейна. На рис. 6.2 изображены функции М(х, β₁) и М (х, β₂). Точки y_β1 и y_β2 являются решениями соответствующих задач вида (6.2), то есть точками абсолютных минимумов функций М(х, β₁) и М(х, β₂). Через у обозначено решение исходной задачи (6.1), то есть точка минимума линейной функции φ(x) на отрезке [a, b]. На рис. 6.2 видно, что при β_k→0 соответствующие точки y_βk стремятся к точке y.

Если задача (6.1) является задачей выпуклого программирования, то есть функция φ(x) выпукла, функции g_i(x) вогнуты, а множество Г выпукло, то функция φ(x), определенная формулой (6.4), будет выпуклой (см. п. 2.10) на множестве Г и задача (6.2) становится задачей о поиске минимума выпуклой функции М (x, β) на выпуклом множестве Г.

Часто задачу

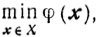
где

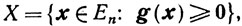
заменяют эквивалентной задачей о минимизации φ(x)

при условиях g(x)- u = 0 u≥0 в качестве штрафа выбирают квадратичную функцию

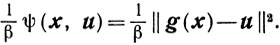
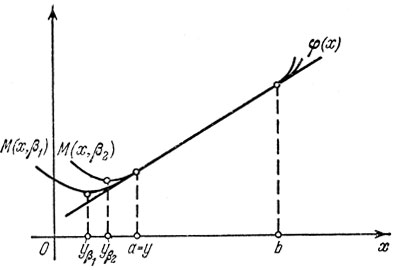
Рис. 6.2

Тогда (6.2) становится задачей о минимизации функции

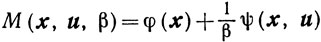
на множестве х∈Е_n, u≥0.

Можно привести еще ряд примеров выбора функции φ(x), например, брать

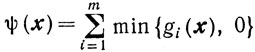
или

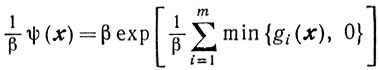
и т. д. Однако выбор штрафа следует согласовывать с методами минимизации функции М(х, β), а значит, как мы увидим из дальнейших глав, следует учитывать гладкость штрафа, простоту вычисления значений функции М (х, β) и ее производных, свойства выпуклости и т. д.

Наконец, о названии метода. Термин "метод штрафных функций" является весьма естественным, поскольку он поясняет суть метода: за нарушение ограничений, то есть когда х∈Г\Х, функция φ(х) "штрафуется" на величину -1/β ψ(х).