6.2. Теоремы о сходимости

Функцию

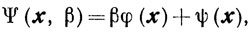
определенную для всех β > 0 на множестве Г, будем называть штрафной функцией задачи (6.1), если ψ(x) удовлетворяет условиям (6.3). Очевидно, что

Заметим, что такой вид штрафной функции несколько затушевывает ее "физический" смысл - штрафование за нарушение ограничений, однако из дальнейшего станет ясным, что при численной реализации методов минимизации функции Ψ (x, β) такой ее вид обладает в ряде случаев преимуществом по сравнению с М (х, β). Пусть точка y_β ∈ Г является решением задачи

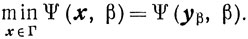
Будем обозначать через y решение задачи (6.1):

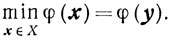
Теорема 6.1. Если существуют y и y_β, то

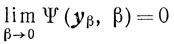(6.5)

и

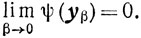(6.6)

Доказательство. 1. Покажем, во-первых, что при β₁ > β₂ > 0 справедливо неравенство

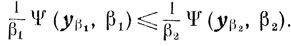(6.7)

Из того, что

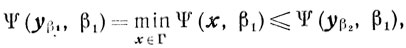
и из неравенства

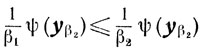
следует

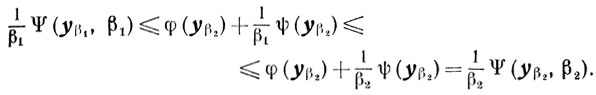
Далее, так как ψ(y) = 0, то

то есть

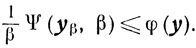
Отсюда и из (6.7) (то есть из монотонности по β функции 1/β ψ(y_β, β))) следует существование конечной величины

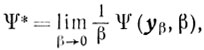
а, значит, и справедливость утверждения (6.5). 2. Покажем сначала, что при β₁ > β₂ > 0

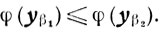(6.8)

Из неравенств

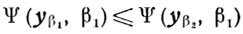
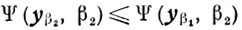
следует

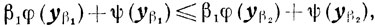
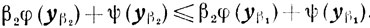
Складывая эти неравенства, получаем

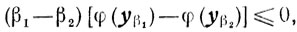
и так как β₁ - β₂ > 0, то

то есть (6.8).

Далее, так как φ(х) ≥ 0, то

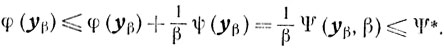
Отсюда и из (6.8) (то есть из монотонности φ(y_β)) следует существование конечной величины

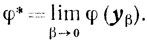
А значит (см. (6.5)),

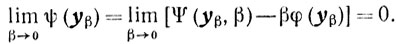
Теорема доказана.

Теперь ясно, что для вычисления значений штрафной функции удобен вид

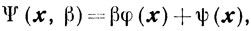
поскольку βφ(y_β)→0 и ψ(y_β)→0 и при вычислении значений Ψ(y_β, β) складываются близкие величины.

При численной реализации метода штрафных функций возникают проблемы выбора начального значения β₀ параметра β и способа изменения _k. Сложность здесь состоит в следующем. Выбор достаточно малого β₀ дает возможность надеяться, что y_β0 будет близким к у. Однако скорость сходимости градиентных методов вычисления точек минимума функции Ψ(x, β), как правило, падает с убыванием величины β. В этом нетрудно убедиться, проанализировав, например, оценку скорости сходимости (9.9), которая линейно зависит от величины 1/L, где L - константа Липшица в формуле

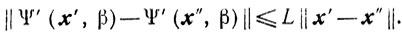
Величина же L оценивается снизу линейной функцией от β: βλ₁+μ₁ (λ₁ - наименьшее собственное число матрицы φ"(x), а μ₁ - наименьшее собственное число матрицы ψ"(x)), убывающей при β→0, а в случае μ₁=0 стремящейся к нулю при β→0.

Таким образом, выбор малого β₀ ведет к близости y_β0 к y, но часто влечет за собой медленную сходимость численных методов минимизации функции Ψ(x, β₀). Выбор же большого ро ведет к обратной картине.

Теорема 6.2.Если

(а) φ(x) и g(x) непрерывны на Г;

(в) существует такой компакт Y⊆Γ, что y_β∈Y, то

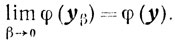
(г) Если, кроме того, элемент у единствен, то

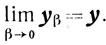
Доказательство. Предположим, что теорема неверна, то есть существует такое число δ > 0 и такая последовательность {_k}→0 при k→∞, что для всех k = 0, 1, ... будет выполняться неравенство

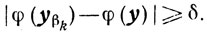
Так как ψ(x)≥0 для всех х, а ψ(y)=0, то

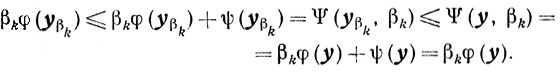(6.9)

Поскольку y_βk∈Y то, не изменяя нумерации, будем полагать, что

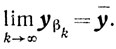
Тогда из (6.9) получаем, что

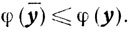
Но ввиду (6.6)

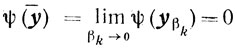
и, следовательно, ȳ∈ X, поэтому приходим к равенству

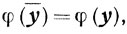
противоречащему предположению. Наконец, пусть элемент у единствен. Предположим, что утверждение (г) неверно, то есть существует такое число δ > 0 и такая последовательность {β_k}→0 при k→∞, что для всех k = 0, 1, ... будет выполняться неравенство

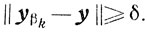
Аналогично предыдущим рассуждениям получаем, что

откуда, ввиду единственности y, следует равенство

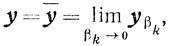
противоречащее предположению.

Теорема 6.3.Если функции g_i(x) вогнуты и непрерывны на выпуклом и замкнутом множестве Г, а функция φ(х) сильно выпукла и непрерывна на Г, то

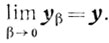
Доказательство. Так как функция

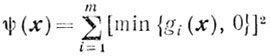
выпукла (см. п. 2.10) и непрерывна, то ввиду сильной выпуклости и непрерывности функции φ (х) будет сильно выпукла и непрерывна функция Χ(x, β), а, следовательно, существуют и единственны точки y и y_β (см. п. 2.13, свойство 2). Из (6.9) следует, что φ(y_β)≤φ(y) а значит, {y_β} - компакт (п. 2.13, свойство 2). Таким образом, все условия теоремы 6.2 выполнены и поэтому y_β→y при β→0.