6.3. Применение метода штрафных функций в линейном программировании

Случай, когда метод штрафных функций применяется к решению задач линейного программирования, интересен оценками, характеризующими скорость сходимости метода.

Рассматривается задача (4.22)

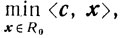
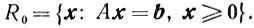
Будем предполагать, что она разрешима, то есть

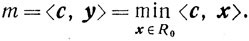
Построим штрафную функцию

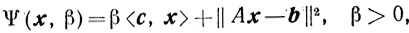
и рассмотрим задачу

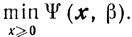(6.10)

Так как по предположению задача (4.22) разрешима, то существует w - решение задачи, двойственной к (4.22), то есть такое, что

Теорема 6.4. Если задача (4.22) разрешима, то существует

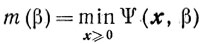
и

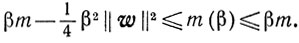(6.11)

Доказательство. Заметим, во-первых, что для Любого x≥0 справедливо неравенство

Далее, для любого x≥0 получаем

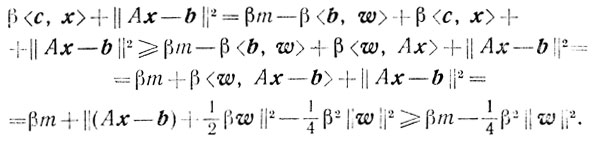
Отсюда следует существование^*

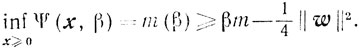
Но

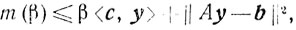
и так как <с, y> = m и

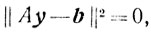
то окончательно приходим к неравенствам (6.11). Пусть y_β-решение задачи (6.10):

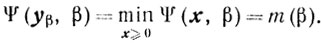
Оценим величину

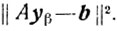
Так как

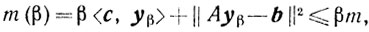
то, воспользовавшись тем, что

получаем

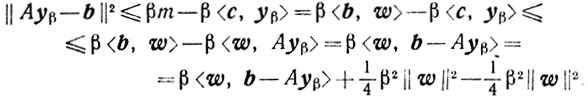
Поэтому

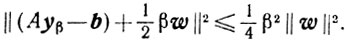
^* (Можно доказать, что если квадратичная функция ограничена снизу на множестве x≥0, то существует y_β≥0 такой, что m(β)=Ψ(y_β, β))

Тогда

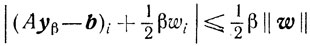
для всех i = 1,..., m. Далее,

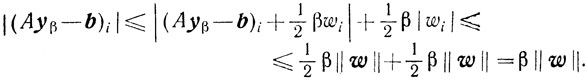
И, следовательно,

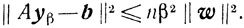(6.12)

Наконец, оценим величину |<c, y_β>-m|. Из (6.11) следует, что

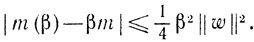(6.13)

Так как

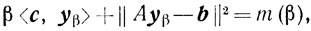
то

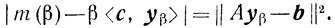
Отсюда и из (6.12) и (6.13) получаем

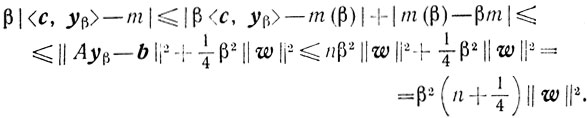
Итак,

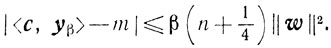(6.14)