Глава 7. Вопросы устойчивости в математическом программировании

7.1. Корректные и некорректные задачи

У значительного числа практических задач, математическими моделями которых являются задачи математического программирования, исходная информация носит приближенный характер. В связи с этим возникает проблема выделения таких классов задач и численных методов минимизации, для которых малые возмущения исходной информации несущественны, то есть не оказывают сильного влияния на решение.

Рассмотрим задачу отыскания таких элементов y∈X, что

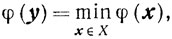(7.1)

где

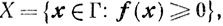
f(x)- векторная функция,

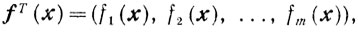
а φ(x) и f_i(x) (i = 1,...,m)- заданные непрерывные скалярные функции.

На практике информация о φ(х) и f(x) носит приближенный характер, то есть вместо φ(х) и f(x) известны такие функции φ_ε(x) и f_ε(х), определенные на множестве Г, что

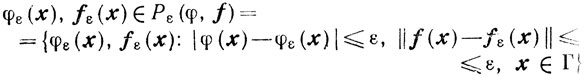
При этом выбор функций _ε и f_ε из множества Ре не заносит от нашего желания. Таким образом, о решении входной задачи судят по решению y_ε приближенной задачи:

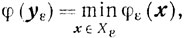(7.2)

где

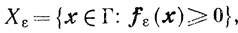
случайно выбранной из класса приближенных задач. Пусть

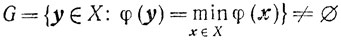
и

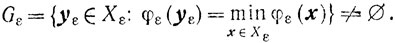
Назовем задачу (7.1) слабо корректной, если

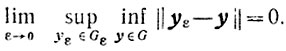(7.3)

Задачу (7.1) будем называть корректной, если

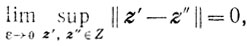(7.4)

где Z = G_ε∪G.

Поясним эти определения. Предельное соотношение (7.3) означает, что семейство множеств G_ε стягивается при ε→0 к множеству, принадлежащему G. На языке "ε, δ" это значит, что для любого δ > 0 найдется такое ε₀ > 0, что для любого ε∈(0, ε₀] и любого y_ε∈G_ε найдется такой y∈G, что ||y_ε-y||≤δ. Отсюда следует, что для любого δ > 0 найдется такое ε₀ > 0, что для любых ε∈(0, ε₀] и φ_ε∈P_ε будет

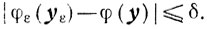
Читателям предоставляется возможность самостоятельно удиться в справедливости этого утверждения.) Таким образом, слабая корректность по сути дела означает ректность по функционалу:

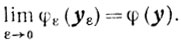
Условие (7.4) означает, что семейство множеств G_ε стягивается при ε→0 к множеству G, состоящему из единственного элемента у. То есть для любого δ > 0 найдется такое ε₀ > 0, что для любого ε ∈ (0, ε₀] и любого y_ε ∈ G_ε будет

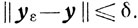
Очевидно, что корректная задача всегда является слабо корректной, но не наоборот.

Будем говорить, что задача (7.1) некорректна, если нарушается условие (7.4).

В случае некорректности задачи (7.1), при заданном ε > 0 всегда найдутся такие пары φ_ε, f_ε и φ̃_ε, f̃_ε, принадлежащие множеству Р_ε(φ, f), для которых решения y_ε и ỹ_ε соответствующих задач вида (7.2) существенно различны и поэтому не несут в себе достаточной информации о решении исходной задачи.

Пример 1. Рассмотрим в Е₂ пару задач:

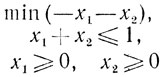(7.5)

и

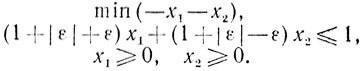(7.6)

Очевидно, что задача (7.5) является слабо корректной и в то же время некорректной. Пример 2.

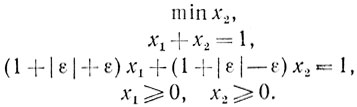(7.7)

Очевидно, что задача (7.7) при ε = 0 будет некорректной и, более того, она не будет слабо корректной.

Основные методы решения задач математического программирования создавались при молчаливом предположении, что задача корректна. Например, процедуру

симплексного метода решения задачи линейного программирования

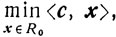
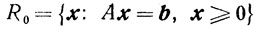
можно интерпретировать следующим образом: на каждом итерационном шаге метода элементы матрицы А и компоненты векторов b и с преобразуются в А', b' и с' по формулам тождественных преобразований (по формулам полного исключения Жордана-Гаусса) и в результате итерационного шага, если все преобразования осуществлять точно, возникает новая задача

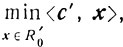
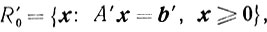
эквивалентная исходной. На практике при вычислениях производят округления, поэтому в реальных случаях итерационный шаг приводит не к эквивалентной задаче, а к новой приближенной задаче. Понятно, что при некорректности решение приближенной задачи может существенно отличаться от решения исходной задачи. В последние годы математики обратились к разработке методов решения некорректных задач. Одним из основных представителей этих методов является так называемый метод регуляризации, в основе которого лежит идея аппроксимации некорректных задач корректными. В связи с этим прежде всего возникает необходимость выделения классов корректных задач.