7.2. Один класс корректных задач
Рассмотрим задачу (7.1) и задачу
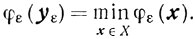 (7.8)
(7.8) Обратим внимание на то, что, в отличие от задали (7.2), в задаче (7.8) допустимое множество то же,что и в задаче (7.1), поэтому здесь
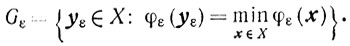
Теорема 7.1.Если функция φ(х) сильно выпукла на множестве X,
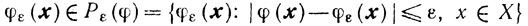
и Gε ≠ 0, то для любого δ>0 найдется такое 0>0, что для всех ε∈(0, ε0] и любых φε(х)∈Pε(φ) будет
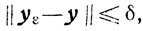
а, следовательно, задача (7.1) корректна.
Доказательство. Ввиду сильной выпуклости функции φ(х) справедливо неравенство (см. (2.24))
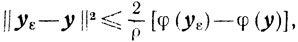 (7.9)
(7.9)где ρ - параметр сильной выпуклости.
ПОСКОЛЬКУ φε(yε)≤φε(y), то
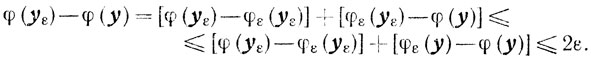
Отсюда и из (7.9) получаем оценку
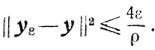
Таким образом,
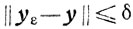
для всех
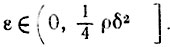
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'