7.3. Задачи с точными ограничениями. Метод регуляризации

Для решения некорректных задач (в том числе и задач линейного программирования) А. Н. Тихоновым был предложен метод регуляризации. В настоящем разделе этот метод рассматривается применительно к задачам нелинейного программирования.

Большинство реальных задач, которые формализуются как задачи математического программирования, содержат дополнительную информацию, позволяющую выбирать устойчивое решение. Во многих задачах типа (7.1) нужно найти элемент множества G, который удовлетворял бы еще некоторым дополнительным условиям; например, был бы ближайшим к некоторой фиксированной точке х°. В задачах оперативного планирования, где у является оптимальным планом, элемент х° обычно характеризует план предшествующего периода, существенное отклонение от которого может быть связано с организационными и технологическими перестройками и, следовательно, сопряжено с дополнительными затратами. Возникает естественная постановка задачи: для заданного х₀∈Е_n найти y°∈G такой, что

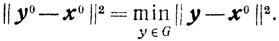
Элемент y⁰ называют нормальным решением задачи (7.1), а саму задачу (7.10)-задачей о нормальном решении.

Процедура регуляризации отыскания нормального решения задачи (7.1) для частного случая, когда возмущена лишь целевая функция (информация о множестве X предполагается точной), состоит в следующем.

Вводится регуляризующая функция

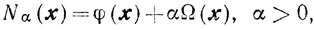(7.11)

где

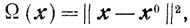
и рассматривается задача отыскания элемента y_α∈Х такого, что

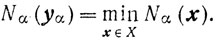(7.12)