7.4. Сходимость
Теорема 7.2.Если функция (х) непрерывна на замкнутом множестве X, а множество G не пусто, то для любого δ > 0 найдется такое α0 (δ) ≥ 0, что для всех α ∈ (0, α0] будет
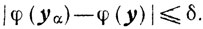
Если, кроме того, выпуклы функция φ(x) и множество X, то
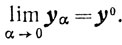
Доказательство. 1) Покажем, что для любого α>0 существует yα. Пусть y0-такой фиксированный элемент из G, что
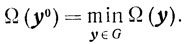
Так как множество G замкнуто, то такой элемент y0 существует. Рассмотрим следующую окрестность точки x0:
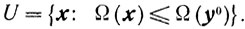
Поскольку множество U ∩ X замкнуто и ограничено, то существует элемент yα такой, что
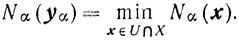
Пусть x∈X\U. Тогда
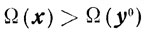
и
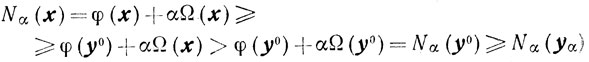
(последнее, правое неравенство справедливо, поскольку y0∈U∩X).
Итак,
Nα(yα)≤Nα(x)
для любого х ∈ X.
2) Так как
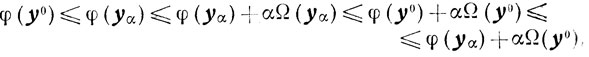
то
Ω(yα)≤Ω(y0) (7.13)
и
φ(y0)≤φ(yα)≤φ(y0)+αΩ(y0)
Переходя в этом неравенстве к пределу при α→0, получаем
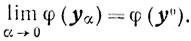
3) Пусть выпуклы φ(x) и X. Тогда выпукло и множество G. В силу (7.13){yα} компакт. Пусть у его произвольная предельная точка
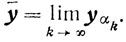
По доказанному
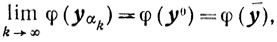
поэтому ȳ∈G. Тогда из (7.13) следует
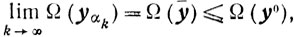
то есть
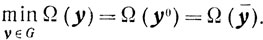
Но сильно выпуклая функция Ω(x) на выпуклом и замкнутом множестве G достигает минимума в единственной точке, а значит ȳ=y0. Таким образом, доказано, что {yα} при α→0 имеет единственную предельную точку, то есть
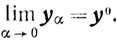
Что и требовалось доказать.
Замечание. Получить априорные оценки скорости приближения yα к y0 в общем случае нельзя. Простые примеры показывают, что скорость приближения yα к y0 при α→0 может быть весьма медленной. Так, для одномерной задачи
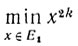
(k≥1)
выбирая х0≠0 в Ω(х) = (х-х0)2, получаем, что yα стремится к y0 = 0 при α→0 со скоростью О(α1/(2k-1)).
В конце настоящей главы мы увидим, что это обстоятельство может оказать существенное влияние на сходимость процесса регуляризации в задачах, когда возмущению подвергается и допустимое множество.
Теорема 7.3.Пусть множество X выпукло и замкнуто; функция φ(х) выпукла и непрерывна; функции φε(x) непрерывны;
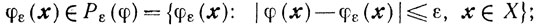
множества G и Gε не пусты; тогда задача (7.12) корректна при любом фиксированном α > 0.
Доказательство. Пусть
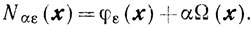
Из условия, что Gε≠∅, и определения функции Ω(х) вытекает существование yαε-решения задачи
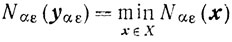
(см. п. 1 доказательства теоремы 7.2).
Легко убедиться, что функции Nα(x) и Nαε(x) удовлетворяют условиям теоремы 7.1, откуда и следует корректность задачи (7.12).
Замечание. Из теоремы 7.1 применительно к Nα(x) следует
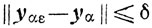
для всех
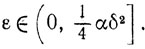
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'