7.5. Метод регуляризации (общий случай)

В предыдущем разделе был рассмотрен метод регуляризации для задач с точными ограничениями, когда возмущению подвергалась лишь целевая функция. Ниже рассматриваются задачи вида (7.2), то есть тот общий случай, когда о задаче (7.1) известна лишь ε-информация, а именно, известны функции φ_ε(х) и f_ε(x) из множества Р_ε(φ, f). Для получения приближенных значений нормального решения задачи (7.1) используется следующая методика.

Вводят параметрическую функцию

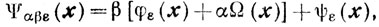
где β > 0 и

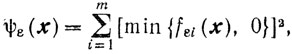
и вычисляют y_αβε∈Γ, решая задачу

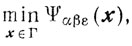
причем в качестве y_αβε может быть взято приближенное значение точного решения задачи минимизации функции Ψ_αβε(x).

Обратим внимание на то, что Ψ_αβε(x) является штрафной функцией для задачи минимизации регуляризующей функции

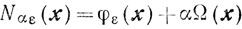
на множестве Х_ε.