8.4. Схемы метода Фибоначчи

Схема 1.

1) Выбираем в качестве n наименьшее натуральное число, удовлетворяющее неравенствам

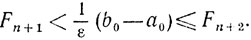
2) 1-й шаг.

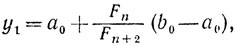
вычисляем φ(y₁) и φ(z₁).

Полагаем

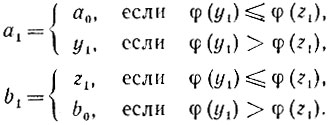
3) k-й шаг (2≤k≤n). Пусть известны

Если φ(y_k-1)≤φ(z_k-1), то вычисляем

и полагаем

Если φ(y_k-1) > φ(z_k-1), то полагаем

и вычисляем

Полагаем

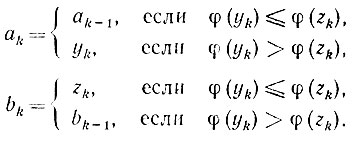
При численной реализации методов одномерной минимизации все вычисления производятся с точностью, лимитируемой возможностями ЭВМ. Численные эксперименты показали, что на окончательный результат вычислений по рассмотренной выше схеме существенным образом влияет точность представления чисел Фибоначчи в памяти машины. Оказалось, что погрешности в вычислениях точек y_k и z_k могут столь быстро накапливаться, что ожидаемая точность решения будет существенно отличаться от реальной.

Существуют схемы метода Фибоначчи, свободные от указанного недостатка. Приведем одну из них.

Схема 2. 1) Выбираем число n так же, как и в схеме 1.

2) 1-й шаг.

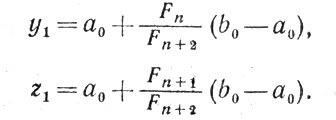
Вычисляем φ(y₁) и φ(z₁).

Числа a₁, b₁ выбираем так же, как и в схеме 1.

3) k-й шаг (2≤k≤n). Пусть известны

Если φ(y_k-1)≤φ(z_k-1), то вычисляем ,

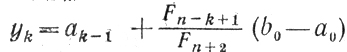
и φ(y_k) и полагаем z_k=y_k-1, φ(z_k)=φ(y_k-1)

Если φ(y_k-1)>φ(z_k-1), то полагаем

и вычисляем

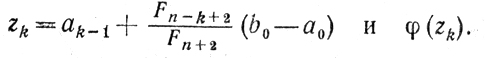
Числа a_k, b_k выбираем так же, как и в схеме 2.