9.4. Методы спуска. Общая схема

Все методы спуска решения задачи безусловной минимизации различаются либо выбором направления спуска, либо способом движения вдоль направления спуска. Это позволяет выписать общую схему методов спуска и исследовать для нее вопросы сходимости и устойчивости.

Итак, решается задача минимизации функции φ(x) на всем пространстве Е_n. Методы спуска состоят в следующей процедуре построения последовательности {x_k}. В качестве начального приближения выбирается, вообще говоря, любая точка х₀∈Е_n. Последовательные приближения х₁, х₂, ... строятся по следующей схеме:

1) В точке x_k выбирают направление спуска-s_k;

2) находят (k + 1)-е приближение по формуле

где в качестве величины β_k выбирают любое число, удовлетворяющее неравенству

Здесь число λ_k - любое такое, что 0<λ_k≤1, а

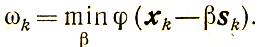
На рис. 9.1 изображен путь от точки х₀ к точке х₁ от х₁ к х₂ и т. д.

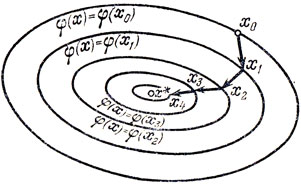
Рис. 9.1

Как правило, в большинстве методов спуска величина λ_k выбирается равной единице. Таким образом, для отыскания β_k приходится решать задачу одномерной минимизации. Естественно, что в реальных ситуациях одномерный минимум вычисляют приближенно, пользуясь, например, одним из методов, рассмотренных в гл. 8. Сходимость релаксационного процесса (если она имеет место) при выборе β_k из условия (9.8), во-первых, показывает устойчивость процедуры спуска к возможным вычислительным погрешностям^*. С другой стороны, численные методы решения задачи одномерной минимизации требуют многократных вычислений значений минимизируемой функции, что часто бывает сопряжено со значительными трудностями, особенно если значение φ(х) определяется в результате некоторого эксперимента. В этой ситуации оказывается иногда целесообразным ограничиться несколькими шагами в сторону убывания φ(x). Именно это и допускает условие (9.8). В самом деле, из неравенства (9.8) следует, что

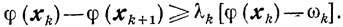
Отсюда и из оценки (9.3) получаем, что

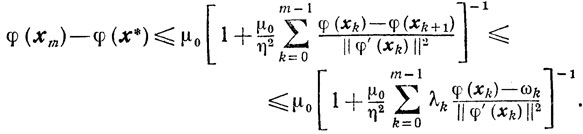
Эти оценки показывают, что до тех пор, пока отношение

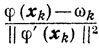
остается сравнительно большим, число вычислений значений φ(х) можно сократить, понизив точность одномерной минимизации, то есть уменьшив допустимую величину λ_k.

^* (Определение устойчивости см. в конце п. 9.1. )

Часто в процессе счета, несмотря на то, что априорные оценки (в предположении, что все λ_k=1) свидетельствуют о сходимости метода со скоростью, скажем, O(1/m), обнаруживается, что с увеличением числа итераций скорость сходимости либо уменьшается, либо вообще процесс перестает сходиться. Одной из причин этого может оказаться потеря точности при вычислении одномерного минимума. Из приведенных выше оценок видно, что неблагоприятная ситуация, когда

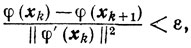
может иногда быть исправлена за счет повышения точности одномерной минимизации, то есть за счет такого допустимого увеличения параметра Х_k, при котором будет выполняться неравенство

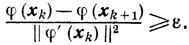
Необходимость повышения точности одномерной минимизации обычно возникает в окрестности точки минимума и при попадании точки х_k в так называемый овраг, то есть когда по некоторым направлениям производная близка к нулю.

Обозначим через α_k величину косинуса угла между направлением антиградиента -φ' (x_k) в точке х_k (то есть направлением наискорейшего убывания функции φ(x) в этой точке) и направлением спуска - s_k из этой же точки:

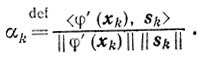
Теорема 9.4.Если

3) последовательность {х_k} строится по формулам (9.7), (9.8), то справедлива оценка

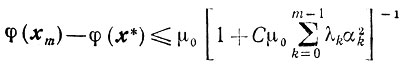(9.9)

для любого 0<С≤1/(2Lη²).

Доказательство. Из (9.7), (9.8) для любых значений параметра β получаем

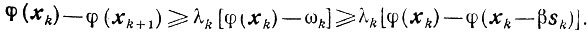
Отсюда, пользуясь леммой 9.3 и определением величины α_k, приходим к неравенству

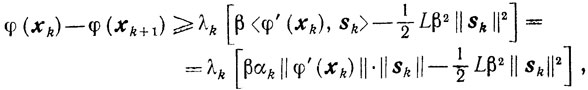
справедливому для любых значений β. Выбирая

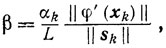
получаем, что

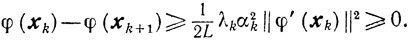(9.10)

Отсюда и из оценки (9.3) получаем (9.9).

Замечание. Если существует такой номер m₀, что α_m0≠0, то из (9.9) (аналогично 9.4) следует неравенство

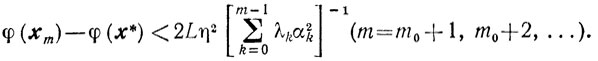(9.11)

Теорема 9.6.Если

2) последовательность {х_k} строится по формулам (9.7), (9.8), то справедливы оценки

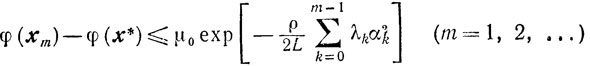(9.12)

и

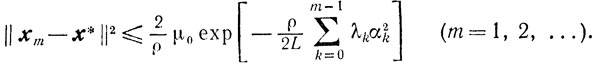(9.13)

Доказательство. Оценки (9.12) и (9.13) с очевидностью следуют из (9.5), (9.6) и (9.10).

Обсуждение. Если направление - s_k выбирается таким образом, что |α_k|≥α>0 для всех k = 0, 1 ..., a λ_k∈[λ, 1], где 0<λ≤1, то из (9.11) получаем, что

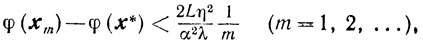
из (9.12) и (9.13) следуют оценки

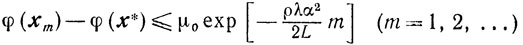
и

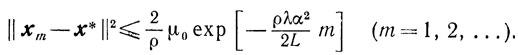
Очевидно, что в смысле этих соотношений наиболее благоприятные оценки возникают при |α_k| = 1 и λ_k = 1.

Заметим, что вычисление одномерного минимума с высокой степенью точности сопряжено обычно с большим числом вычислений минимизируемой функции (вспомним методы из гл. 8), что часто снижает эффективность выбранного процесса минимизации.

Второй способ для определения величины β_k. Как правило, наиболее трудоемкой частью численной реализации методов спуска является отыскание величины β_k. В связи с этим важное значение приобретают различные подходы к решению этой задачи.

Будем в качестве β_k выбирать наибольшее из чисел, удовлетворяющих неравенствам

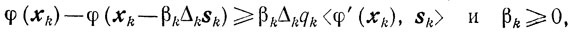(9.14)

где числа q_k-любые из полуинтервала (0, 1/2] , а

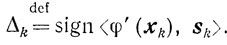
Роль чисел q_k поясняется в конце настоящего пункта. Во-первых, покажем, что существует β̄_k, удовлетворяющее неравенствам (9.14). Действительно, если выбрать

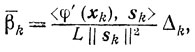
то, пользуясь леммой 9.3 и тем, что Δ²_k=1, получаем соотношение

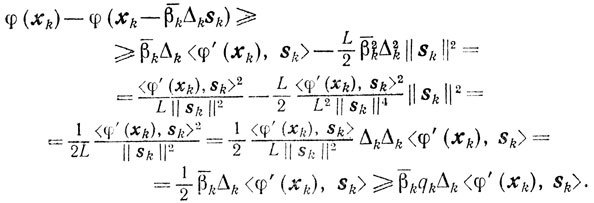
Задача отыскания наибольшего элемента, удовлетворяющего неравенствам (9.14), иногда оказывается более простой по сравнению с задачей одномерной минимизации, которую приходится решать, чтобы удовлетворить условиям (9.8). Например, можно воспользоваться следующим элементарным способом отыскания β_k. Выбирают некоторое начальное значение β_k0≥0. Если при этом первое из неравенств (9.14) нарушается, то уменьшают величину β_k0, например, вдвое до тех пор, пока β_ki=1/2ⁱβ_k0 не удовлетворит условиям (9.14). Этот процесс можно продолжить, увеличивая β_ki до тех пор, пока

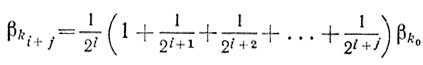
не нарушит условия (9.14) и т. д.

Сходимость. Оценить скорость сходимости метода спуска при выборе величины β_k из условий (9.14) не представляет труда.

Теорема 9.6.Если

3) последовательность {x_k} определяется соотношениями (9.7) и (9.14), то

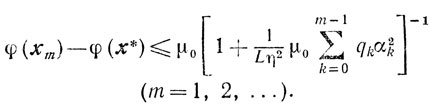(9.15)

Если, кроме того, функция φ(х) сильно выпукла^*, то

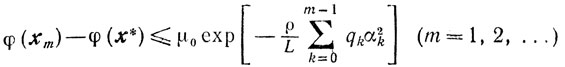(9.16)

и

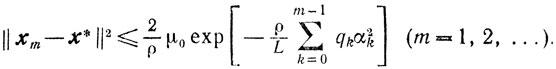(9.17)

Доказательство. Поскольку β_k-наибольшее из чисел, удовлетворяющих неравенствам (9.14), а

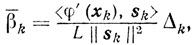
как мы видели, удовлетворяет этим неравенствам, то β_k≥β̄_k, и из (9.14), учитывая определение α_k, получаем

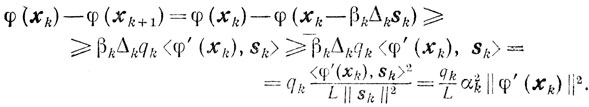
Ввиду этого из неравенств (9.3), (9.5) и (9.6) следуют искомые оценки.

^* (Условие 2) при этом становится излишним (см. п. 2.13, свойство 2). )

Обсуждение. Если бы была известна L-константа Липшица, то условие, чтобы величина β_k была наибольшей из всех, удовлетворяющих неравенствам (9.14), можно ослабить, потребовав, чтобы было

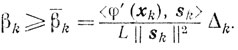
В частности, можно выбирать β_k = β̄_k. Однако, как правило, в реальных случаях определить величину L-задача слишком сложная, если вообще выполнимая.

Рассмотрим влияние точности в определении величины β_k из условий (9.14) на скорость сходимости релаксационного процесса. Пусть q_k=1/2, k = 0, 1, ...; предположим, что в результате процедуры поиска β_k найдено такое его приближенное значение, что

Тогда, пользуясь леммой 9.3, получаем

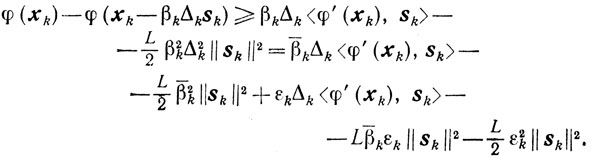
Но

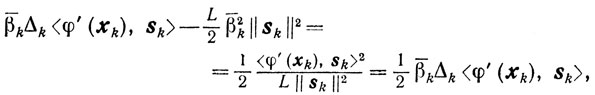
а

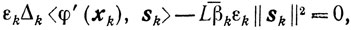
вследствие чего

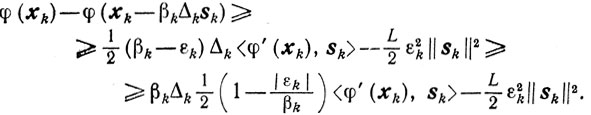
Если величина ε_k столь мала, что вторым слагаемым в правой части неравенства можно пренебречь, то условия (9.14) будут выполняться при

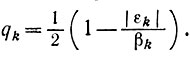
В свою очередь оценки (9.15) - (9.17) показывают существенную зависимость сходимости процесса от величины суммы

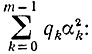
если направления спуска -s_k выбираются таким образом, что все

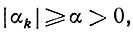
то

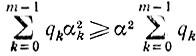
и, следовательно, чем ближе к 1/2 все значения q_k, то есть чем выше точность в определении величины β_k, тем выше скорость сходимости, которую гарантируют наши оценки.