9.5. Метод градиентного спуска

Оценки скорости сходимости (9.9), (9.12), (9.13), (9.15)-(9.17) показывают, что весьма удачным может оказаться такой выбор направления спуска - s_k, при котором α_k = 1. Ясно, что если s_k = φ' (x_k), то

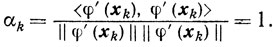
В пользу такого выбора направления спуска можно привести и следующие неформальные соображения. Поскольку антиградиент, то есть - φ' (x_k), в точке х_k указывает направление наискорейшего убывания функции, то естественным представляется сместиться из точки x_k по этому направлению.

Метод спуска, в котором s_k = φ'(x_k), называют методом градиентного спуска.

Схема 1 итерационной процедуры метода градиентного спуска такова. В качестве начального приближения может быть выбрана любая точка х₀∈Е_n. (k + 1)-е приближение x_k+1, исходя из найденного значения х_k, строится по формуле x_k+1 = x_k-β_ks_k где s_k = φ' (х_k), а в качестве β_k выбирается число, удовлетворяющее неравенству

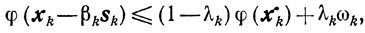
где 0 <λ≤λ_k≤1, а

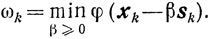
В дальнейшем мы будем пользоваться следующей краткой записью:

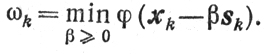(9.19)

Теорема 9.4 дает следующую оценку скорости сходимости схемы 1 метода градиентного спуска:

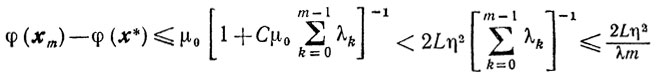
а в случае сильной выпуклости функции φ (x) из теоремы 9.5 получаем

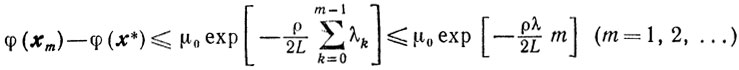
и

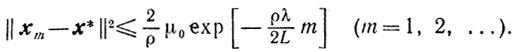
В случае, когда λ_k = 1, то есть β_k определяется в результате одномерной минимизации:

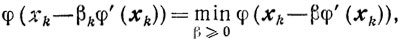
релаксационный процесс называют методом скорейшего спуска.

Для φ(х) ∈ С¹ (E₂) метод скорейшего спуска имеет геометрическую интерпретацию: точка x_k+1 является точкой касания луча

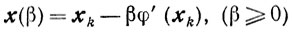
с линией уровня

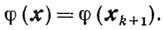
Схема 2.

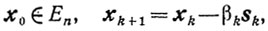(9.7)

β_k:

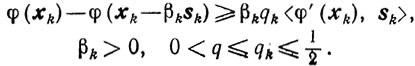(9.19)

В качестве β_k здесь (как и в условиях (9.14)) выбирается наибольшее число, удовлетворяющее неравенствам (9.19). Заметим, что по сравнению с (9.14) здесь, в (9.19), опущен сомножитель

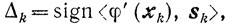
поскольку здесь всегда Δ_k = 1.

Теорема 9.6 дает для этой схемы следующие оценки скорости сходимости: для выпуклой функции φ(x) будет

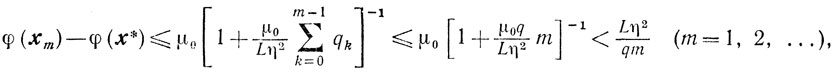
а в случае сильной выпуклости функции φ(x) оценки приобретают вид

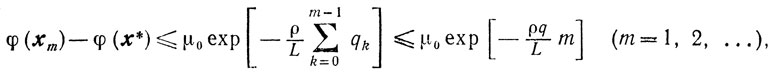
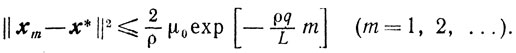
Априорные оценки скорости сходимости методов спуска показывают существенную зависимость скорости сходимости градиентного спуска от точности вычислений φ' (x_k) и величины β_k. Потеря точности, а это обычное явление в окрестности точек минимума либо в овражной ситуации, может вообще нарушить сходимость релаксационного процесса градиентного спуска. В этом случае, если не представляется возможность повысить точность вычислений, возникает необходимость попытаться воспользоваться другими методами, которые, в отличие от метода градиентного спуска, учитывают, кроме свойств выпуклости, и другие свойства минимизируемой функции.