9.6. Метод сопряженных направлений
Существует класс методов, по своей вычислительной сложности мало отличающийся от методов градиентного спуска, который минимизирует строго выпуклые квадратичные функции за конечное число шагов (итераций). Этому классу принадлежит так называемый метод сопряженных направлений*. Предположение, что выпуклая функция φ(x) в окрестности точки минимума обладает свойствами, вообще говоря, близкими к свойствам квадратичной функции, послужило основанием для применения метода сопряженных направлений в задачах минимизации общего вида.
* (Читателю, знакомому с вычислительными методами линейной алгебры, этот метод известен как метод сопряженных градиентов решения систем линейных алгебраических уравнений вида Ах=b, а следовательно, как метод минимизации квадратичной функции φ(x) = ||Ax-b||2(см. [1]).)
Схема метода.
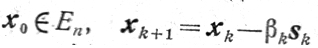 (9.7)
(9.7)(k = 0, 1, ...),
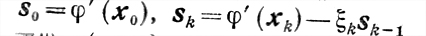 (9.20)
(9.20)(k = 1, 2, ...),
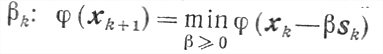 (9.21)
(9.21) (k = 0, 1, ...).
Различные варианты метода сопряженных направлений отличаются способом выбора параметра ?А. Заметим, что если все k = 0, то рассматриваемая схема превращается в схему метода скорейшего спуска, поскольку условие (9.21) в этом случае является условием (9.8)
при λk = 1.
Условие (9.21) выбора величины βk определяет следующие две особенности последовательности {xk}.
Лемма 9.4.Для дифференцируемой функции φ(х) последовательность {xk}, построенная по схеме (9.7), (9.20), (9.21) такова, что выполняются следующие соотношения:
 (9.22)
(9.22)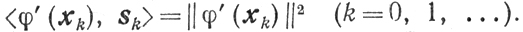 (9.23)
(9.23) Доказательство. Из условия (9.21) следует, что при βk > 0 будет
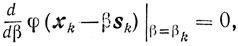
а при βk = 0 (см. теорему 2.12) будет
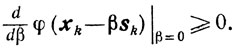
Если βk > 0, то
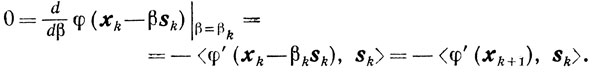
Доказательство того, что соотношение (9.22) справедливо и для βk = 0, будем проводить по индукции. Если β0 = 0, то из х1 = х0 и s0 = φ'(x0), получаем
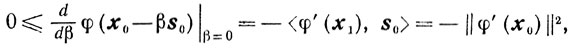
откуда следует равенство
<φ'(x1, sk)>=0
Пусть справедливо соотношение <φ'(xk, sk-1)>=0. Докажем, что
<φ'(xk+1, sk)>=0
при βk = 0. Так как xk+1 = xk, то из (9.20) получаем
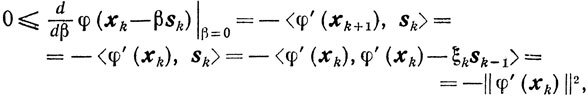
откуда и следует (9.22).
Наконец, соотношение (9.23) является очевидным следствием равенств (9.20) и (9.22).
В следующей теореме устанавливаются условия выбора параметра ξk, гарантирующие сходимость метода сопряженных направлений со скоростью того же порядка, что и в методах градиентного спуска.
Теорема 9.7. Если
1) выпуклая функция φ(х) принадлежит классу
2) diam X0 = η<∞;
3) последовательность {хk} строится по схеме (9.7), (9.20), (9.21);
4) найдется неотрицательное число С≥0, для которого выполняется соотношение
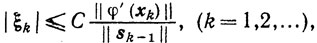 (9.24)
(9.24)то справедлива оценка
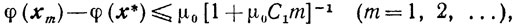
где
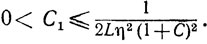
Если, кроме того, функция φ(x) сильно выпукла, то
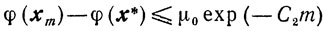
и
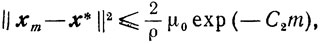
где
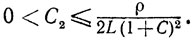
Доказательство. Из (9.20) и (9.24) получаем неравенство
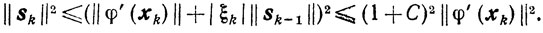
Отсюда и из (9.23) следует, что
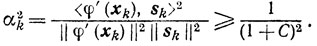
Поскольку последовательность {xk} удовлетворяет всем условиям теорем 9.4 и 9.5 (условие (9.21) эквивалентно условию (9.8) при λk = 1), то оценки (9.9), (9.12) и (9.13) сразу приводят к желаемому результату.
Заметим, что теорема 9.7 дает оценки, гарантирующие сходимость метода сопряженных направлений, но не выявляет его достоинств, а именно конечности метода, когда функция φ(х) квадратична.
Рассмотрим три способа выбора параметра ?А, обеспечивающие конечность метода в квадратичном случае.
Способ 1.
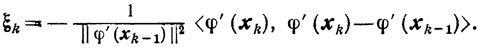
Предположим, что функция φ(x) сильно выпукла. Тогда из (2.21) получаем
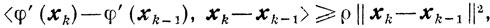
откуда, учитывая (9.7), (9.22) и (9.23), следует неравенство
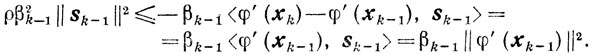
Так как мы всегда предполагаем, что для всех k = 0, 1, ... будет φ' (xk) ≠ 0, то из доказательства леммы 9.4 вытекает, что βk > 0, поскольку из βk-1 = 0 следует || φ' (xk-1)|| = 0. Итак,
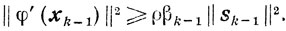
Учитывая это и условие
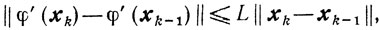
оценим величину ξk:
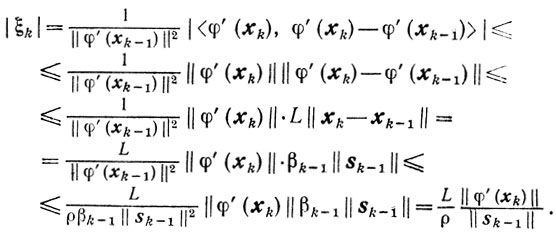
Таким образом, выполняется условие (9.24) и поэтому из теоремы 9.7 получаем оценки

и
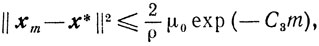
где
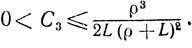
Способ 2.
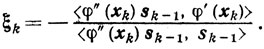
Этот способ выбора параметра ξk едва ли можно признать эффективным, поскольку он сопряжен с вычислением на каждой итерации матрицы φ"(xk)- процедуры весьма трудоемкой. Однако элементарный анализ сходимости полезен своей методической стороной, поскольку аналогичная методика приемлема для оценок скорости сходимости так называемых методов квазиньютоновского типа*, многочисленные варианты которых содержатся в различных статьях и не перестают появляться в математической литературе до последнего времени.
* (См., например, [4] . )
Предположим, что сильно выпуклая функция φ(x) дважды непрерывно дифференцируема с равномерно ограниченной нормой матрицы φ" (х) на ограниченном множестве
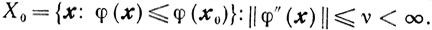
||φ"(x)||≤ν<∞
Так как
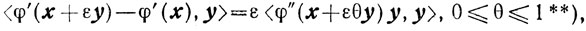
** (См., например, [9].)
то, учитывая свойство сильной выпуклости (2.21), получаем, что
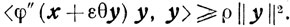
Переходя в этом неравенстве к пределу при ε→0, приходим к соотношению
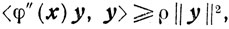 (9.25)
(9.25)справедливому для любого y ∈ Еn. Вследствие этого получаем
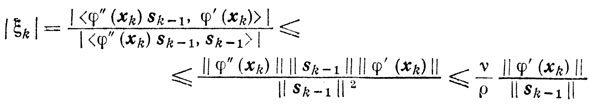
и поэтому из теоремы 9.7 получаем оценки
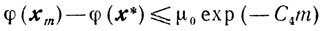
и
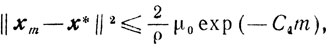
где
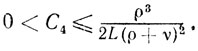
Способ 3 (см. [11]).
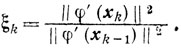
Для оценки скорости сходимости в случае, когда функция φ(x) сильно выпукла, докажем ряд утверждений.
Утверждение 1. Для всех k = 1, 2,... имеет место соотношение
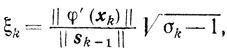
где
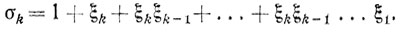
Доказательство. Из (9.20) и (9.22) получаем,
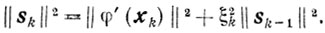
Пользуясь этим, покажем, что
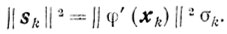
Действительно, для k=1 это равенство очевидно. В индуктивном предположении, что оно справедливо для k>1, покажем его справедливость для k+1 так как 1 + ξk+1k = σk+1 то
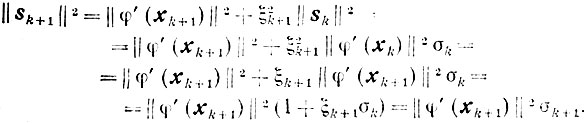
Для завершения доказательства используем полученные соотношения
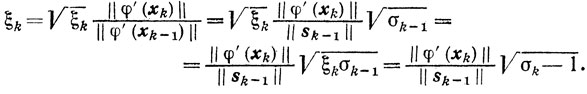
Утверждение 2.Для любого номера k=1, 2, ... справедливо неравенство
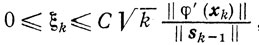
где
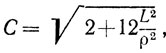
L-константа Липшица в условии φ(x) ∈ С1,1 (En), а ρ-параметр сильной выпуклости.
Доказательство. Так как функция φ(x) сильно выпукла, принадлежит классу С1,1(Еn) и, кроме того, φ{хm}≤φ{xp} для всех m≥p и р = 0, 1, ..., то из формулы (2.27) (см. п. 2.13, свойство 4) имеем
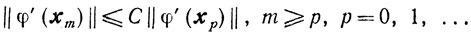
Но
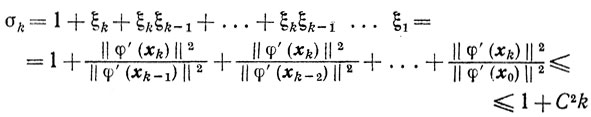
и поэтому
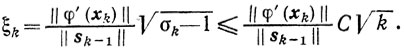
Утверждение 3. Для последовательных приближений, построенных по способу 3, имеют место оценки
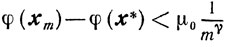
и

справедливые для всех
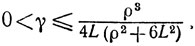
Доказательство. Из (9.20), (9.22), (9.23) и утверждения 2 следует
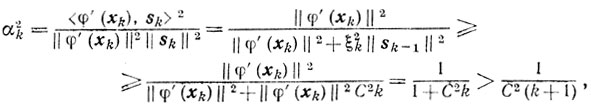
вследствие чего
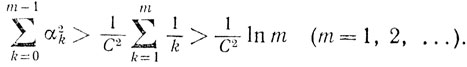
Отсюда и из (9.12) и (9.13) при λk=1 получаем, что
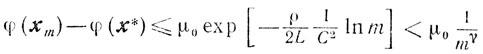
для всех
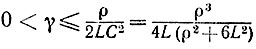
и
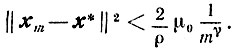
Обсуждение. Хотя приведенные оценки справедливы для всех m = 1, 2, ... и гарантируют определенную скорость сходимости метода сопряженных направлений, однако, как уже говорилось, они не выявляют тех преимуществ метода, что для строго выпуклой квадратичной функции φ(x) каждый из трех приведенных способов определения величины k приводит к тому, что метод дает решение задачи за конечное число шагов, превосходящее величины n - размерности пространна Еn. Этот факт, доказательство которого читатель случае необходимости может найти, например, в [2], играет существенную роль в использовании метода для решения задач минимизации не квадратичных функций. А именно по методу сопряженных направлений делают n итераций, после чего производят так называемое обновление метода, полагая ξn = 0, то есть осуществляют градиентный спуск. Таким образом, схема метода в этом случае будет выглядеть так:
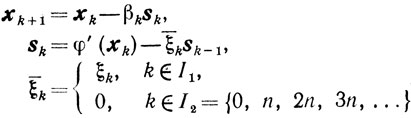
и
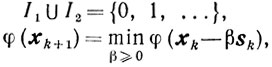
а величина ξk определяется из соображений конечности метода в квадратичном случае, например, одним из приведенных выше способов. Это так называемая n-шаговая схема.
Наконец, следует отметить, что метод сопряженных направлений весьма чувствителен к ошибкам, возникающим в процессе счета, поскольку при λk≠1 нарушается свойство ортогональности (9.22) и тем самым нарушается свойство конечности метода в квадратичном случае.
Рассмотренные методы безусловной минимизации носят название методов первого порядка, поскольку при определении направления спуска в них существенно знание первой производной-градиента функции φ(x). Однако процедура вычисления градиента часто бывает весьма трудоемкой и тем самым снижается эффективность этих методов. Методы, которые излагаются в последующих разделах настоящей главы, не требуют вычисления градиента функции. Правда, априорные оценки свидетельствуют о более низкой скорости сходимости этих методов по сравнению с методами первого порядка, однако этот недостаток в ряде случаев компенсируется простотой вычисления направления спуска.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'