9.7. Покоординатный спуск
Будем на каждой итерации в качестве направления спуска-sk выбирать направление вдоль одной из координатных осей. В этом разделе приводится схема, не обладающая достоинствами независимости выбора направления спуска от градиента функции, но зато имеющая оценки, гарантирующие сходимость процесса минимизации со скоростью порядка O(1/m). Эти оценки интересны тем, что показывают существенную зависимость скорости сходимости от размерности пространства Еn. Пусть xk уже известен, и пусть
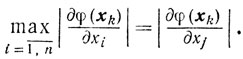
Можно считать, что
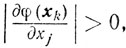
так как в противном случае xk = x* и процесс минимизации оканчивается. Схема метода:
xk+1=xk-βksk (9.7)
sk = ej-координатный вектор
βk: φ(xk-βksk)≤(1-k)φ(xk)+λkωk, 0<λ≤k≤1 (9.8)
где
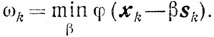
Выясним скорость сходимости метода, предполагая, го функция φ(x) удовлетворяет условиям, при которых справедлива теорема 9.4, а в случае сильной выпуклости-теорема 9.5. Так как
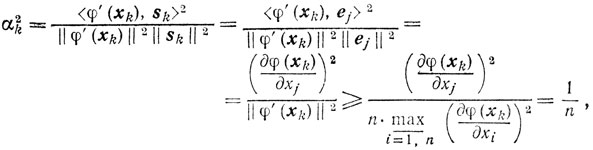
то из (9.9) получаем оценку
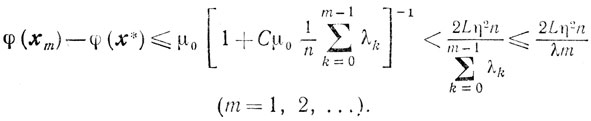
(m=1, 2,....)
Таким образом, константа при величине 1/m в оценке скорости сходимости этого метода в п раз больше соответствующей константы в оценках метода градиентного
спуска.
В случае же сильной выпуклости функции φ(x) из (9.12) и (9.13) получаем оценки
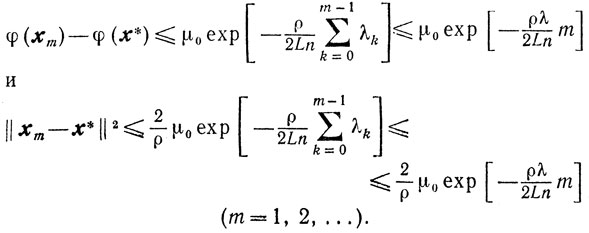
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'