9.8. Циклический покоординатный спуск

В этом методе выбор направления спуска не зависит от информации о градиенте минимизируемой функции: сначала спускаются по направлению e₁ затем-по е₂ и т. д., вплоть до е_n, после чего весь цикл повторяют снова.

Этот метод часто применяют на начальной стадии процесса минимизации. Простой алгоритм метода и отсутствие необходимости вычислять направление спуска делают его весьма перспективным методом получения начального приближения для более точных методов минимизации.

Существует и другая сторона целесообразности использования метода циклического покоординатного спуска, а именно получение масштабных множителей для преобразования переменных. Поясним это подробнее.-Рассмотрим простой пример. Пусть

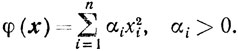
Если числа α_i сильно различающиеся, то линии (поверхности) уровня функции φ(x) сильно вытянуты по тем направлениям е_i которым соответствуют малые значения α_i. Тогда при движении вдоль направления антиградиента (метод градиентного спуска) смещение в направлении точки минимума будет довольно медленным Заменой переменных x_i = μ_iy_i можно добиться того, чтобы в новых переменных y_i линии уровня стали сферами.

Для этого нужно взять μ_i=α_i^-1/2 В новых переменных точка минимума для квадратичной функции находится градиентным методом за одну итерацию. Преобразование x_i=α_i^-1/2y_i называют изменением масштабов.

В случае, если φ(x) гладкая выпуклая функция выбирают

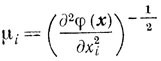
в точке х одномерного минимума вдоль направления e_i. Множитель μ_i пропорционален радиусу кривизны линии уровня в точке х. И хотя это преобразование не превратит в сферы линии уровня, но уменьшит их вытянутость и тем самым облегчит применение градиентных методов минимизации.

Величины

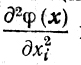
вычисляют приближенно, пользуясь

их конечно-разностной аппроксимацией. Метод циклического покоординатного спуска как раз и позволяет получать последовательные приближения величин масштабных множителей μ_i.

Опишем схему метода.

Первый цикл.

Исходя из произвольной точки х₀, строят

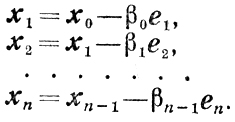
Второй цикл.

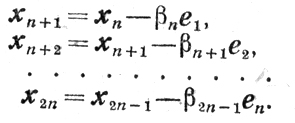
l-й цикл.

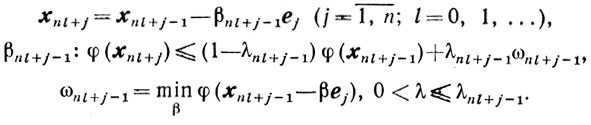
Величину β можно определять и другими способами, например, по формулам (9.14). Заметим, что если применение метода циклического покоординатного спуска не ставит целью вычисление масштабных множителей, то обычно величину шага β выбирают постоянной, изменяя ее лишь в том случае, когда этот выбор становится неудачным.

Сходимость метода для выпуклых функций из класса С^1,1(Е_n) со скоростью порядка O(1/m) можно гарантировать, ввиду оценок предыдущего пункта, лишь для n=2. В то же время нетрудно доказать, что если последовательность {x_k} сходится, то в ее предельной точке х будет φ' (x) = 0.

Теорема 9.8.Если функция φ(x) принадлежит классу С^1,1(Е_n), а последовательность {х_k}, построенная методом циклического покоординатного спуска, сходится при k→∞ к точке х, то φ'(x̄) = 0 и, следовательно, точка х является стационарной^*.

Доказательство. Запишем последовательность {x_k} следующим образом:

где j(k) принимает соответствующие значения 1, 2, ..., n. Пользуясь леммой 9.3 и определением β_k, получаем (аналогично тому, как это делалось в предыдущем пункте)

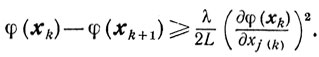
Так как последовательность {x_k} сходится, то φ(x_k)-φ(x_k+1)→0 при k→∞ и ∂φ(x_k)/∂x_j(k)→0 при k→∞.

^* (Для выпуклой функции φ'(x) точка х будет точкой минимума. )

В предельной точке х̄ будет φ' (х̄) = 0. В самом деле, если предположить, что по некоторому направлению e_i будет

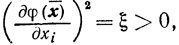
то в достаточно малой окрестности этой точки будет

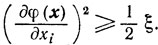
Но так как, начиная с некоторого номера k₀, все точки x_k попадут в нашу окрестность, то последнее неравенство противоречит тому, что

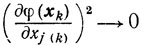
при k→∞.

В п. 9.11 сходимость метода циклического покоординатного спуска будет доказана в более слабых предположениях.