9.9. Случайный покоординатный спуск
Более перспективным по сравнению с предыдущими является покоординатный спуск, в котором направление спуска выбирается случайным образом. При таком подходе к выбору направления существуют априорные оценки, гарантирующие в выпуклом случае с вероятностью, стремящейся к единице при m→∞, сходимость процесса со скоростью порядка O(1/m), а в случае сильной выпуклости - с экспоненциальной скоростью.
Процедура k-то шага этого процесса выглядит следующим образом: из n чисел {1, 2, ..., n} выбирается случайным образом номер j (k) и в качестве sk выбирается единичный координатный вектор ej(k), после чего осуществляется спуск.
Схема 1.
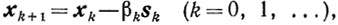 (9.7)
(9.7) 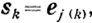 (9.27)
(9.27)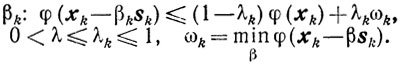 (9.8)
(9.8)Схема 2.
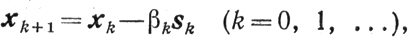 (9.7)
(9.7)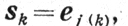
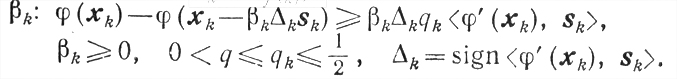 (9.14)
(9.14)В доказательстве сходимости релаксационных процессов, устанавливаемых этими схемами, мы будем пользоваться следующими очевидными свойствами, вытекающими из аксиом теории вероятностей.
Пусть u, v и w-случайные величины. Тогда из равенств Р {u≤v} - 1 и Р {v≤w} = 1 следует равенство
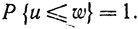 (9.28)
(9.28)Если Р{u≤v}=*1, а Р {v≤w} = p, то
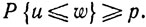 (9.29)
(9.29)Теорема 9.9.Если
1) выпуклая функция φ(x) принадлежит классу С1,1 (En);
2) diam X0 = η<∞;
3) последовательность {xk} строится либо по схеме 1, либо по схеме 2, то
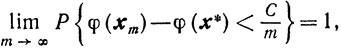
где
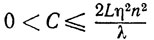
в случае схемы 1 и
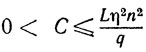
в случае схемы 2.
Если кроме того, функция φ (x) сильно выпукла, то
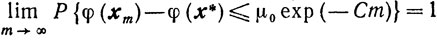
и
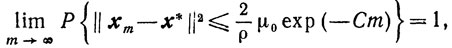
где
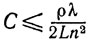
в случае схемы 1 и
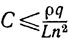
в случае схемы 2.
Доказательство. Пусть j1, j2, ..., js-такие номера, что 1≤j1<j2<....<js≤n и
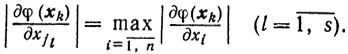
Так как j(k)-случайная величина такая, что
p{j(k) = i} = 1/n при i = 1, 2, ..., n,
то индикатор случайной величины j (k)
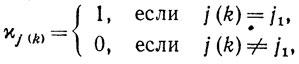
принимает значение, равное единице, с вероятностью 1/n. Поскольку j(0), j(1), ...-последовательность взаимно независимых случайных величин, то χj(0), χj(1),... также взаимно независимы. При χj(k) = 1 имеем
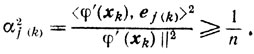
Далее
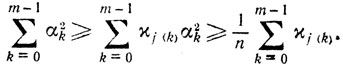 (9.30)
(9.30)По закону больших чисел для любого ε>0
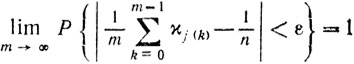
или
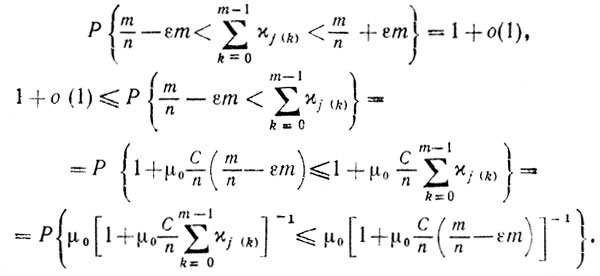 (9.31)
(9.31)Из теорем 9.4 и 9.6 следует, что
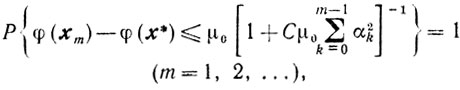
(m=1, 2,...)
где 0<C≤λ/2Lη2 в случае схемы 1 и 0<C≤q/L2 в случае схемы 2. Поскольку неравенство (9.30) означает, что
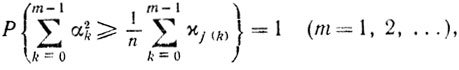
то свойство (9.28) приводит нас к равенству
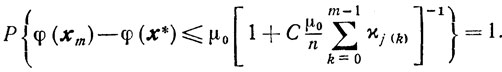
Отсюда и из (9.31) с учетом (9.29) получаем
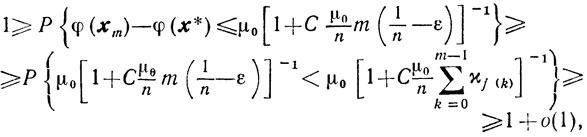
следовательно
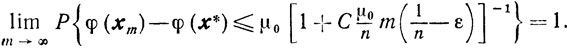
Если же функция φ(x) сильно выпукла, то соответствующие оценки следуют из теорем 9.5 и 9.6.
Обратим внимание на то, что здесь по сравнению с соответствующими оценками теорем 9.4, 9.5 и 9.6. константа С увеличилась в n2 раз.
При доказательстве теоремы 9.9 для простоты были сделаны предположения, от которых не представляет труда избавиться. А именно целесообразно индикатор χj(k) определять так:
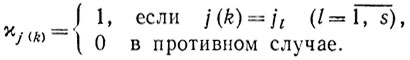
И, кроме того, номер j(k) следует выбирать не из п чисел {1, 2, ..., n}, а из (n-1) чисел {1, 2, ..., j (k-1)-1, j (k-1) + 1, ...,n}, поскольку на(k + 1)-м шаге нет смысла спускаться по направлению -sk-1. Очевидно, что величина константы-С в соответствующих оценках в этом случае уменьшится.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'