9.10. Метод случайного спуска
Один из весьма распространенных релаксационных методов случайного поиска минимума дает следующий способ построения последовательности {xk}.
На n-мерной единичной сфере с центром в начале координат выбирается случайная точка sk, подчиняющаяся на этой сфере равномерному распределению, и затем по вычисленному на k-м шаге процесса элементу хk определяется хk+1 по формуле (9.7).
Схема 1.
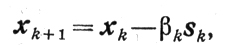
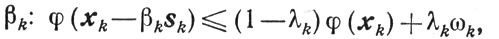 (9.8)
(9.8)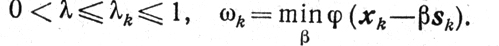
Схема 2.
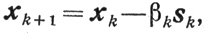 (9.7)
(9.7)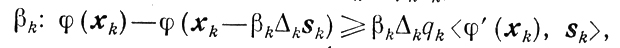 (9.14)
(9.14)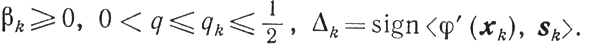
Обратимся к исследованию сходимости последовательности {xk}, построенной по одной из этих схем.
Определение. Случайный вектор s∈En называется равномерно распределенным на квадрируемой поверхности S, если для всякого измеримого подмножества S' (S'⊆S)
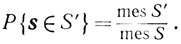
Здесь символ "mes" означает площадь.
Пусть
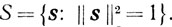
Поскольку при ортогональном преобразовании Q единичная сфера переходит в себя (QS ≡ S) и, кроме того, mes S'= mes QS' для любого S' ⊆ S, то для любой ортогональной матрицы Q случайный вектор Qs равномерно распределен на S, если равномерно распределен на 5 случайный вектор s.
Пусть lT = (l1, ..., ln) - произвольный единичный вектор (||l||2=1). В таком случае, если s-случайный вектор, равномерно распределенный на S, то скалярное произведение <l, s> имеет тот же закон распределения, что и любая компонента вектора s (например, s1). Действительно, рассмотрим ортогональную матрицу Q, первая строка которой совпадает с lT. Выше констатировано, что Qs имеет то же распределение, что и s, то есть первая компонента вектора Qs, равная , имеет то же распределение, что и s1 Но распределение s1 от l не зависит, следовательно, если l-случайный единичный вектор, то условное распределение <l, s> (при заданном l) совпадает с безусловным распределением s1 Это означает, что <l, s> не зависит (в вероятностном смысле) от I: P {<l, s>≤ξ|l} = Р {s1 ≤ ξ}, ξ∈E1.
Таким образом, плотность вероятности случайной величины <l, s> совпадает с плотностью вероятности случайной величины s1 Обозначим эту плотность ps1(ξ), где, очевидно, -1≤ξ≤+ 1. Таким образом,
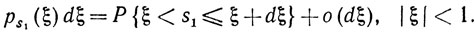
Но
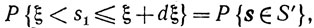
где S' - кольцо на сфере S, расположенное между плоскостями с уравнениями s1=ξ и s1 = ξ + dξ (рис. 9.2). Площадь сферы радиуса r в m-мерном пространстве равна Сmrm-1, где Сm-постоянная. Таким образом, mes S = Cn и площадь сферы радиуса √(1-2) в пространстве размерности n-1 равна Cn-1(1-ξ2)(n-2)/2 Но именно такая сфера и служит "основанием" кольца S' на единичной сфере S. Отсюда следует, что
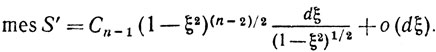
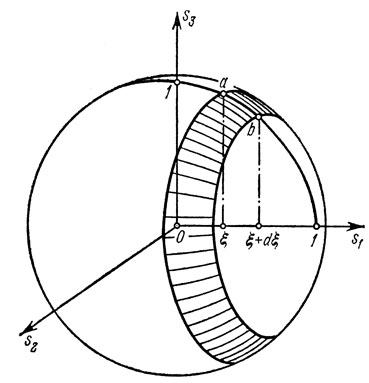
Рис. 9.2
Итак,
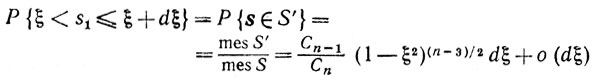
или, что то же самое, ps1 (ξ)dξ = C(1 - ξ2)(n-3)/2dξ, где С не зависит от ξ и определяется условием
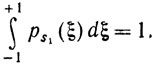
Найдем теперь плотность ps21 (ξ) вероятности случайной величины s21 (0<ξ<1). Поскольку
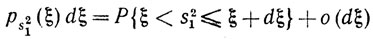
и распределение s1 симметрично относительно нуля (ps21(ξ)=ps1(-ξ)), то
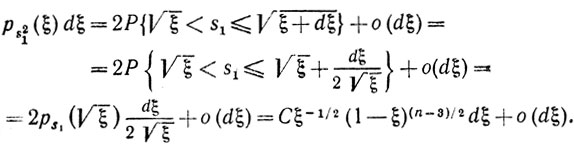
Иными словами,
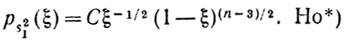
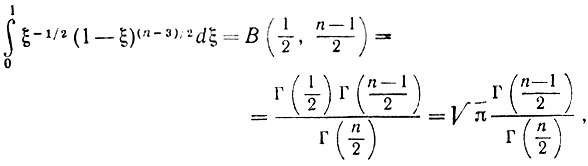
поэтому окончательно получаем
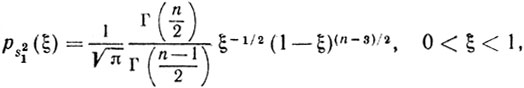
и, как мы убедились,
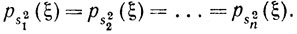
* (О гамма-функциях Г и бета-функциях В см. на стр. 201, )
Так как моменты m-го порядка случайной величины s2i суть
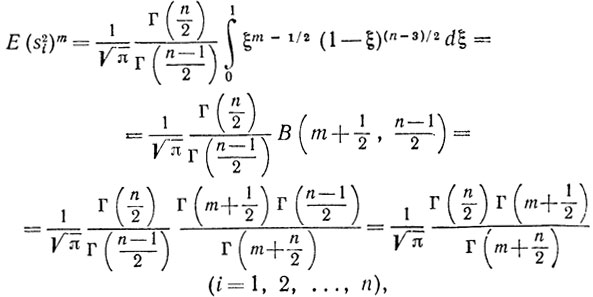
то, в частности,
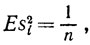
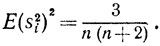
Теперь не представляет труда вычислить дисперсию случайной величины s2i:
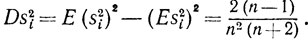
Пусть l0, l1, ..., lk, ... - последовательность случайных единичных векторов, a s0, s1, ..., sk, ...- последовательность взаимно независимых случайных векторов, равномерно распределенных на единичной сфере S (последовательности {lk} и {sk} предполагаются независимыми). Обозначим αk = <lk, sk>. В результате предыдущих рассмотрений доказана следующая теорема.
Теорема 9.10.Случайные величины α0, α1, ..., αk,... взаимно независимы, квадрат каждой из них имеет распределение с плотностью ps21(ξ) и
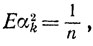
(k = 0,1,...).
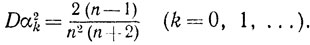
Выше мы пользовались некоторыми свойствами гамма-функций:
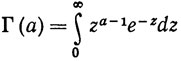
и бета-функций:
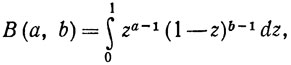
известными из курса математического анализа. В частности, что
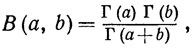
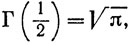
Г(а+ 1) = аГ(а).
Теорема 9.11.Если
1) выпуклая функция y(х) принадлежит классу
2) diam X0 = η<∞;
3) последовательность {xk} строится либо по схеме 1, либо по схеме 2, то для любого действительного m справедлива при m→∞ оценка
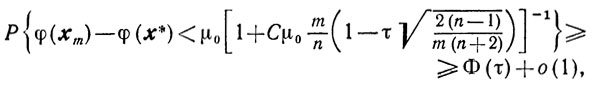
где
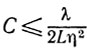
в случае схемы 1 и
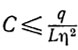
в случае схемы 2, а
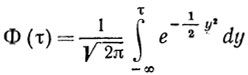
- нормальная функция распределения.
Доказательство. Как и прежде,
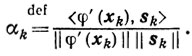
Из доказанных утверждений (если положить
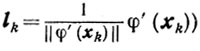
следует, что случайные величины α20, α21, ... взаимно независимы, одинаково распределены в-интервале (0, 1), причем
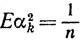
и
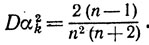
Согласно центральной предельной теореме
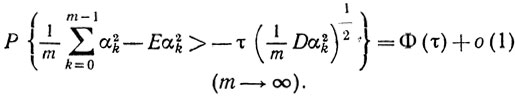
В нашем случае это соотношение принимает вид
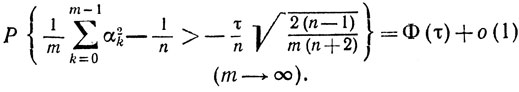
Отсюда в результате элементарных преобразований получаем
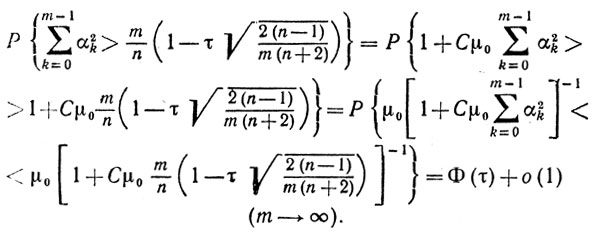
Из теорем 9.4 и 9.6 следует, что
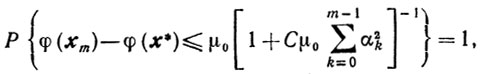
где
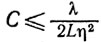
в случае схемы 1 и
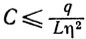
в случае схемы 2. Воспользовавшись свойствами (9.28) и (9.29), получаем окончательно
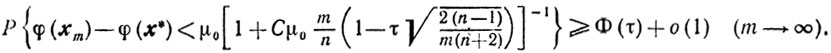
Замечание 1. В последней оценке константа С в n раз превосходит соответствующую константу в оценке скорости сходимости метода градиентного спуска и в n раз меньше соответствующей константы в оценке скорости сходимости метода случайного покоординатного спуска.
Замечание 2. Если функция φ(x) сильно выпукла, то, пользуясь той же методикой, не представляет труда показать, что с вероятностью, стремящейся к единице при m→∞, будет xm→x* с экспоненциальной скоростью.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'