9.11. О сходимости релаксационных методов для не выпуклых задач

Как мы видели, в случае, когда функция φ(х) выпукла и принадлежит классу С^1,1(E_n), удается получить оценки скорости сходимости для большинства рассмотренных выше методов минимизации. Ставится вопрос, при каких условиях на не выпуклую функцию φ(x) методы спуска остаются сходящимися. При этом речь идет не об оценках скорости сходимости, а лишь о факте сходимости.

Будем предполагать, что функция φ(x) непрерывна и что не пусто замкнутое множество Х^* = {х^*: φ(x^*)= min φ (х)}. Обозначим через р=р(х) проекцию точки х на множество X^*:

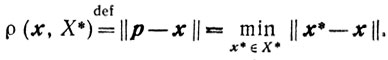
Для ε > 0 определим множество

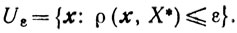
Пусть последовательность {x_k} такова, что

Теорема 9.12.Если для всякого ε>0 найдется такое число η = η (ε) > 0 и такая последовательность {x_k} ⊆ {x_k}, для членов которой, не принадлежащих U_ε, выполняется неравенство

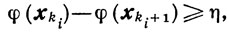
то найдется такой номер k₀ = k₀(η), что x_ki∈U_ξ (k_i≥k₀+1) и, следовательно,

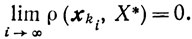
Доказательство. Так как последовательность {φ(х_k)} сходящаяся (ввиду ее монотонности и ограниченности снизу числом φ(x^*)), то найдется такой номер k₀=k₀(η), что для всех k_i≥k₀+1 будет

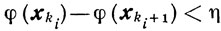
и, следовательно, x_ki∈U_ε (k_i≥k₀+1).

Рассмотрим общую процедуру методов спуска:

где х₀-любая точка из Е_n, a s_k-направление в точке х_k, способами выбора которого различаются методы. Число β_k будем определять из соотношений

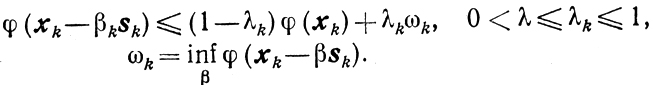
Предположим, что функция φ(x) удовлетворяет условиям:

1) φ(x)∈С^1,1(E_n);

2) для любого ε > 0 найдется такое δ = α (ε) > 0, что ||φ'(х)||≥δ для всех х∉U_ε.

Эти условия означают, что у гладкой (в смысле С^1,1) функции φ(x), достигающей минимума в пространстве Е_n (условие не пустоты множества X^*), отсутствуют точки локальных минимумов (условие 2). Более того, условие 2 накладывает определенные ограничения даже на класс выпуклых функций.

Из соотношений, определяющих величину β_k, и из условия 1, ввиду леммы 9.3, получаем (см. 9.10) оценку

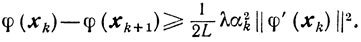
Теорема 9.13.Если направление s_k выбирается таким образом, что α²_k≥α²>0 (k = 0, 1, ...), то

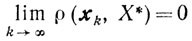
и

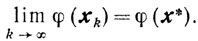
Доказательство. Из условия 2 и предыдущей оценки следует, что для любого ε>0 и всех x_k∉U_ε будет

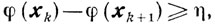
где

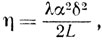
а значит, по предыдущей теореме

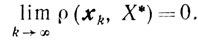
Пользуясь формулой конечных приращений, получаем

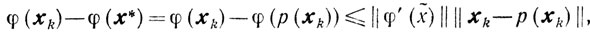
где x̃∈[х_k, р(х_k)]. Отсюда, учитывая условие 1 и то, что φ' (р(х_k)) = 0, приходим к неравенству

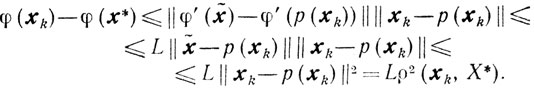(9.33)

Поэтому

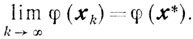
Применим эту теорему для установления сходимости некоторых методов минимизации, предполагая, что φ(x) удовлетворяет условиям 1 и 2.

Метод градиентног отпуска. Здесь s_k = φ'(x_k) (см. п. 9.5). Сходимость метода очевидна, ввиду того, что α_k=1, (k = 0, 1, ...).

Метод случайного спуска (см. п. 9.10). Здесь в качестве s_k выбирается случайная точка на единичной сфере, подчиняющаяся на ней равномерному распределению.

Если для любого ε>0 найдется такая подпоследовательность {x_ki}, что x_ki∈U_ε, то

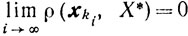
значит, согласно (9.33)

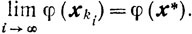
Отсюда, ввиду сходимости последовательности

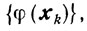
получаем

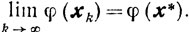
Предположим, что такой последовательности нет. Тогда существует такое ε>0, что, начиная с некоторого номера k₀ = k₀(ε), будет

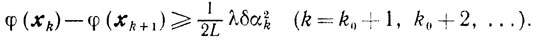
Пусть номер k₁ = k₁ (η) ≥ k₀ таков, что для всех k > k₁ будет

Так как x̃_k∈U_ε, то по условию ||φ'(x_k)||≥δ и, ввиду (9.32), справедливо неравенство

Но, согласно закону "нуля или единицы" вероятность появления такого случайного номера k≥k₀+1 что α²_k≥α>0 (для достаточно малого α∈(0, 1/n)), равна единице (см. теорему 9.10), и поэтому с вероятностью, равной единице, наступит событие

противоречащее предположению. Таким образом,

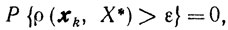
вследствие чего

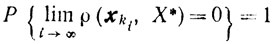
и

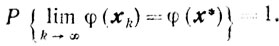
Циклический покоординатный спуск. Для обоснования сходимости требование ||φ'(x)||≥δ при x∉U_ε усилим следующим. Предположим, что для всякого ε>0 в последовательности {x_k}, где x_k+1=x_k-β_ke_j(k) (см. п. 9.8), найдется такая Подпоследовательность {х_k}, для членов которой, не принадлежащих U_ε, выполняется неравенство

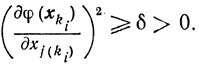
Так же как и в п. 9.7, из леммы 9.3 и определения величины δ получаем для x_ki∉U_ε неравенство

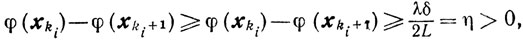
из которого на основании теоремы 9.12 получаем

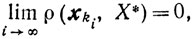
а значит, согласно (9.33)

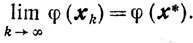
Замечание об условиях существования оценок скорости сходимости. В случае, когда для выпуклой функции φ(x) выполняются условия 1 и 2, справедливы оценки скорости сходимости методов спуска, в том числе градиентного спуска и метода сопряженных направлений, а так же методов случайного покоординатного спуска и метода случайного спуска, аналогичные тем, которые приводились в пп. 9.4,9.5,9.9,9.10. При этом константы в этих оценках будут иными, но порядок скорости сходимости остается прежним. Подчеркнем, что ранее всегда требовалась ограниченность множества

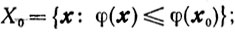
здесь же это требование заменится условием 2.