10.1. Метод условного градиента
В этом методе идея выбора направления спуска состоит в следующем: в точке хk линеаризуют функцию φ(x), строя линейную функцию φL(х) = φ(хk) + <φ'(xk), x-xk> и затем минимизируя φL(x) на множестве X, находят точку yk. После этого полагают - sk=yk-xk и далее вдоль этого направления осуществляют спуск. Таким образом, для отыскания направления - sk следует решить задачу минимизации линейной функции на множестве X. В общем случае это задача того же порядка сложности, что и исходная, однако, когда допустимое множество задается линейными ограничениями, она становится задачей линейного программирования, конечномерные методы решения которой рассматривались в гл. 5.
Прежде чем приступить к исследованию конкретных схем метода условного градиента, рассмотрим следующую достаточно общую процедуру построения минимизирующей последовательности {хk}.
Построение начинается с произвольной точки х0∈Х. Предположим, что уже найден элемент хk∈Х. Для построения элемента
xk+1=xk-βk(xk-yk)∈X
(k = 0, 1,2,...) (10.1)
необходимо определить yk и βk. Относительно yk будем полагать, что
yk∈Х, (10.2)
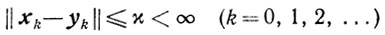 (10.3)
(10.3) и, кроме того,
<φ'(xk), xk-yk>≥0 (k = 0,1,2,...). (10.4)
Пусть βk удовлетворяет неравенствам
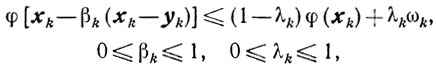 (10.5)
(10.5)где
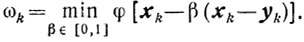
Теорема 10.1.Если на выпуклом и замкнутом множестве X выполняются условия:
1) выпуклая функция φ(x) принадлежит классу C1,1(X);
2) достигается min φ (х) = φ (х*), х* ∈ X;
3) || φ' (х) || ≤γ<∞ для всех х∈Х;
4) последовательность {xk} определяется условиями (10.1)-(10.5), то справедлива оценка
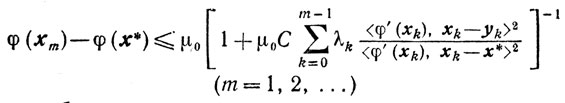 (10.6)
(10.6)для любого положительного числа
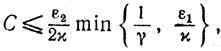
где
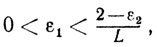
0<ε1<2
Доказательство. Из условий (10.5) и леммы 9.3 получаем следующее неравенство, справедливое для всех β∈[0, 1]:
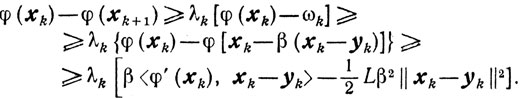 (10.7)
(10.7)В частности, это неравенство справедливо для
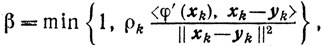 (10.8)
(10.8)где
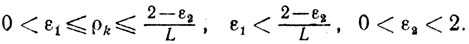 (10.9)
(10.9)Рассмотрим две возможности.
Если β = 1, то из (10.8) следует, что
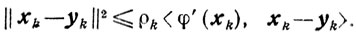
Отсюда и из (10.7) получаем, учитывая (10.3) и условие 3), неравенство
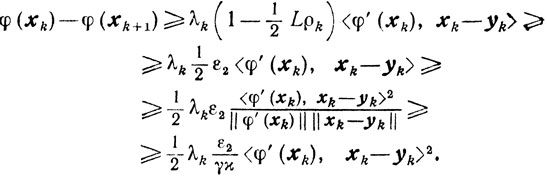 (10.10)
(10.10) Если
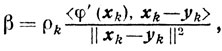
то из (10.7), с учетом условий, определяющих ρk, получаем
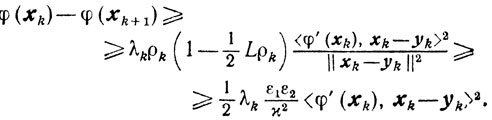
Пусть
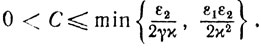 (10.11)
(10.11)Тогда из (10.10) и (10.11) приходим к неравенству
φ(xk)-φ(xk+1)≥Cλk<φ'(xk), xk-yk>2
Поскольку в условиях настоящей теоремы справедлива и теорема 9.1, то последнее неравенство и оценка (9.2) приводят к (10.6).
Замечание. Условия 2) и 3) теоремы 10.1 и условие (10.3) можно заменить требованием ограниченности и замкнутости выпуклого множества X.
Следствие 1.Если в условиях теоремы 10.1 точка yk такова, что
<φ(xk), xk-yk>≥σkk<φ'(xk), xk-x*>
σk>0 (k = 0, 1, ...), (10.12)
то из (10.6) следует оценка
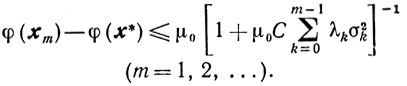 (10.13)
(10.13)Условия (10.12) позволяют при отыскании точки yk приближенно решать задачу
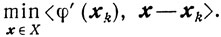
При этом величина σk как раз и характеризует точность в определении приближенного решения этой задачи.
Если в условиях (10.5) и (10.12) λk и σk таковы, что λk≥λ>0, и k≥σ>0, то из (10.13) получаем неравенство
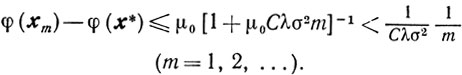 (10.14)
(10.14)Следствие 2.Если в условиях теоремы 10.1 параметр βk определять не соотношениями (10.5), а условиями (10.8), (10.9), то оценки (10.6), (10.13) и (10.14) сохраняют силу при λk=1.
Будем в дальнейшем предполагать, что выпуклое и замкнутое множество X ограничено. Во всех известных схемах метода условного градиента точка yk определяется в результате решения следующей экстремальной задачи:
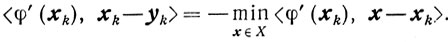 (10.15)
(10.15) Схема 1.
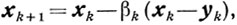 (10.1)
(10.1)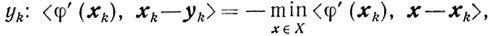 (10.15)
(10.15)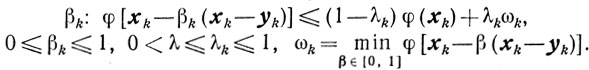 (10.5)
(10.5)Здесь величина ωk является минимальным значением функции φ(x) на отрезке [хk, yk]. Заметим, что величину ωk можно всюду дальше определять из условия
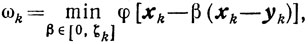
где
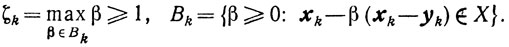
Все последующие результаты останутся при этом справедливыми. Однако дополнительные усилия для определения величины ζk на практике себя не оправдывают.
Сходимость. Так как выполнены все условия теоремы 10.1 и первого следствия при σk=1, то из (10.14) получаем оценку
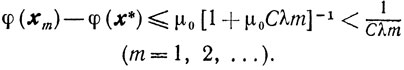 (10.16)
(10.16)Устойчивость. Если yk удовлетворяет условию
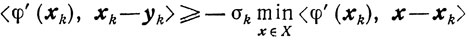 (10.17)
(10.17)при 0<σk≤1, а λk определяется соотношениями (10.5), го из следствия 1, поскольку выполняется условие 10.12), получаем, что справедлива оценка (10.13), а при λk≥λ>0 и σk≥σ>0 выполняется неравенство (10.14). Таким образом, метод устойчив к возможным вычислительным ошибкам в пределах, допускаемых соотношениями (10.17) и (10.5).
Схема 2.
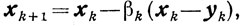 (10.1)
(10.1) 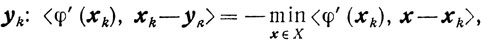 (10.15)
(10.15) 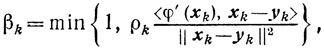 (10.8)
(10.8)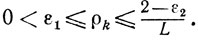 (10.9)
(10.9)Сходимость. Из следствия 2 получаем оценки скорости сходимости (10.13) и (10.14) при σk=1, справедливые для этой схемы.
Устойчивость. Если yk удовлетворяет условию (10.17), а значит, и (10.12), то из следствий 1 и 2 приходим к выводу, что имеют место оценки (10.13) и (10.14) при λk=1. Таким образом, метод устойчив к возможным вычислительным ошибкам.
Схема 3.
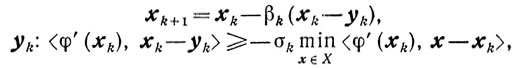 (10.1)
(10.1) 0<k≤1 (10.17)
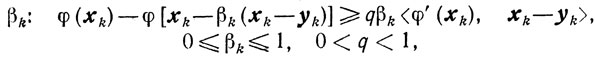 (10.18)
(10.18)где βk-наибольшее из чисел, удовлетворяющих этим условиям.
Вначале покажем, что существуют βk, удовлетворяющие условиям (10.18). Пусть βk определяется соотношениями (10.8), (10.9). Тогда из неравенства (10.7) при λk=1 получаем, повторяя выкладки доказательства теоремы 10.1, для βk=1 (аналогично (10.10))
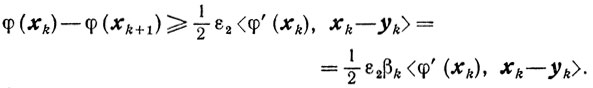
А для
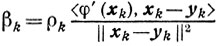
аналогично (10.11) получаем
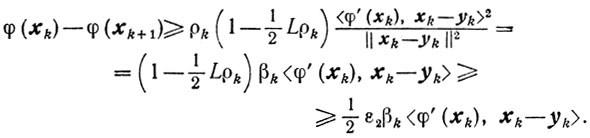
И поскольку ε2 должно удовлетворять неравенству 0<ε2≤2, то условие (10.18) выполняется для любого 0<q≤ε2/2<1.
Сходимость. Из (10.17) и (10.18) следует неравенство
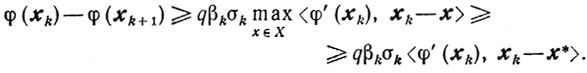
Отсюда и из (9.2) получаем оценку
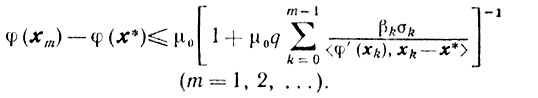
(10.19)
Пусть β̄k наибольшее из чисел, удовлетворяющих условиям (10.18), а βk = τkβ̄k, где 0<τk≤1. В этом случае при β̄k=1 получаем, что
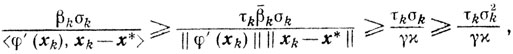
где
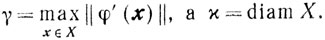
Если же
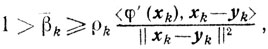
то
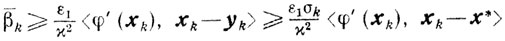
и поэтому
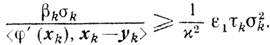
Окончательно из (10.19) получаем оценку
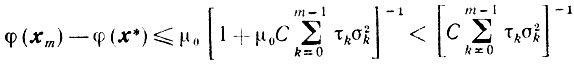 (10.20)
(10.20)справедливую для любого
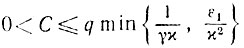
Таким
образом, при 0<τ≤τk≤1 и 0<σ≤σk≤1 приходим к неравенству
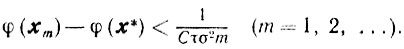 (10.21)
(10.21)Устойчивость метода следует с очевидностью из приведенных оценок.
Случай неограниченности множества X. В предыдущих схемах предполагалось существование решения экстремальной задачи (10.15), то есть задачи выбора направления. Однако это существенно сужает класс задач, к которым применим метод условного градиента. Рассмотрим схему, свободную от этого ограничения, то есть допускающую неограниченность множества X.
Схема 4.
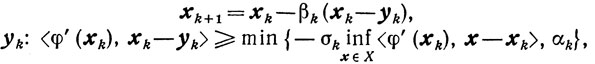 (10.1)
(10.1)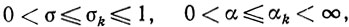 (10.22)
(10.22)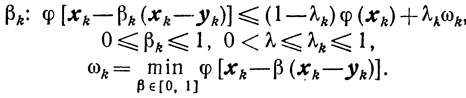 (10.5)
(10.5)Смысл условий 10.22 поясняется в разделе "обсуждение".
Ниже, из оценок скорости сходимости, станет ясным вопрос о выборе величин αk.
Сходимость. Будем предполагать, что
diam Х0 = η < ∞,
где Х0 = {х∈Х: φ(x)≤φ(x0)}, и что существует такое число и, что
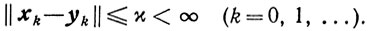
Если
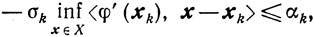
то из (10.22) получаем неравенство
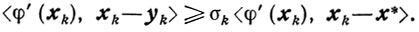
Если же
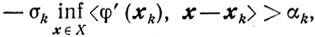
то
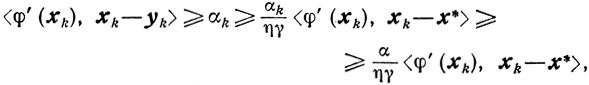
где
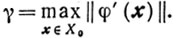
Пусть
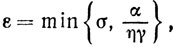
тогда для yk справедливо соотношение

Отсюда и из оценки (10.6) приходим при λk≥λ>0 к неравенству
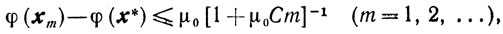
где
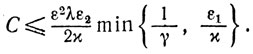
Обсуждение. Ясно, что с уменьшением величины С ухудшается априорная оценка сходимости этого метода. Для того чтобы выяснить вопрос выбора αk, оценим величину С: при некоторых естественных предположениях* справедливо неравенство
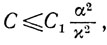
где С1= const > 0. Поскольку величина ||хk-yk|| зависит от выбора α и, следовательно, χ зависит от α, то соотношения, оценивающие величину С, показывают, что αk целесообразно выбирать таким, чтобы отношение aα2k/||xk-yk||2 не убывало с увеличением числа k.
Рассмотрим наиболее перспективный случай применения метода условного градиента, а именно, когда множество X задается системой линейных равенств и неравенств, и задача отыскания yk из условий (10.17) становится задачей линейного программирования. Условия (10.17) и (10.22) позволяют при решении задачи отыскания yk в данном случае задачи линейного
программирования-ограничиться несколькими симплексными шагами, например, обрывая симплексную процедуру в тот момент, когда впервые выполнится (10.17) или (10.22).
* (Например, при χ > 1, 1 ≤1/γ и α/ηγ<1)
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'