10.2. Метод проекции градиента

Как уже говорилось, в случае задач безусловной минимизации весьма распространенным релаксационным методом является метод градиентного спуска. Однако для задач с ограничениями направление спуска вдоль антиградиента не обязательно является возможным. Для отыскания возможного направления в точке х_k напрашивается мысль спроектировать точку v_k = x_k-ν_kφ'(х_k) (ν_k-некоторое фиксированное положительное число) на множество X и в качестве направления спуска взять - s_k=p(v_k)-x_k где P(v_k) - проекция v_k на X, после чего осуществлять спуск вдоль этого направления.

Итак, метод проекции градиента состоит в вычислении проекции p(v_k) точки

на множество X и построении точки

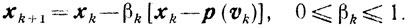(10.23)

Для отыскания направления s_k = x_k - p(v_k) следует решить задачу минимизации квадратичной функции ||v_k-x||² на множестве X. В общем случае это задача того же порядка сложности, что и исходная, однако для задач, когда допустимое множество имеет простую геометрическую структуру, например, является многомерным параллелепипедом, отыскание p(v_k) производится путем сравнения n чисел.

Исследования сходимости и устойчивости различных схем метода проекций градиента основываются на двух теоремах об оценках, при доказательстве которых используются следующие свойства проекции точки на множество. Из (2.2) следует, что

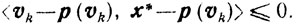(10.24)

А из следствия к теореме 2.2 вытекает, что для любого v_k > 0 справедливо неравенство

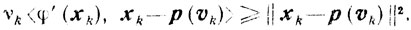(10.25)

Наконец, напомним, что если функция φ(х) выпукла и дифференцируема на выпуклом и, замкнутом множестве X, то из условия x_k=p(v_k) следует экстремальность точки х_k (теорема 2.16). При исследовании сходимости мы всегда будем предполагать, что x_k≠p(v_k), то есть φ(х_k)≠φ(х^*).

Теорема 10.2.Если на выпуклом и замкнутом тожестве X выполняются условия:

4) последовательность {х_k} является релаксационной, то есть

то справедлива оценка:

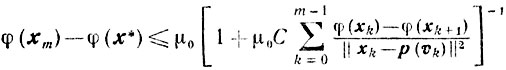(10.26)

при любом

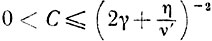
где

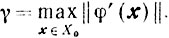
Доказательство. Для того чтобы получить неравенство (10.26), достаточно показать, что

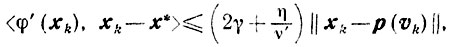
и воспользоваться оценкой (9.2) из теоремы 9.1.

Сначала сделаем следующие тождественные преобразования:

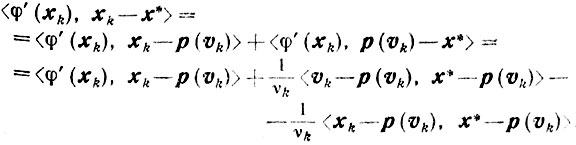
Отсюда и из (10.24) получаем

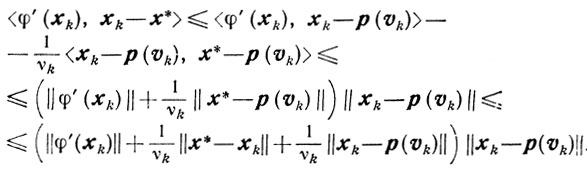
Но из (10.25) следует неравенство

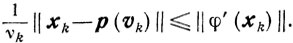
Учитывая, что

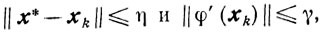
получаем окончательно

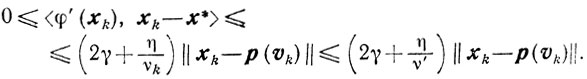
Отсюда и из неравенства (9.2):

получаем оценку (10.26). Теорема доказана.

Рассмотрим теперь последовательность {х_k}, элементы которой строятся по формуле

а y_k и _k удовлетворяют следующим условиям:

где

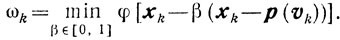
Подчеркнем, что при построении элементов этой последовательности {х_k} выбор y_k, β_k достаточно произволен, лишь бы выполнялись требования (10.28) и (10.29).

Теорема 10.3.Если на выпуклом и замкнутом множестве X:

А) числа v_k таковы, что 0<ν'≤ν_k≤ν"<∞, то справедлива оценка

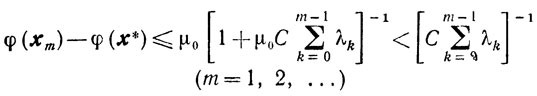(10.30)

при любом

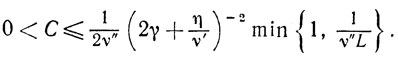
Доказательство. Из леммы 9.3 и неравенства (10.25) получаем, что для любых β∈[0, 1] справедливо соотношение

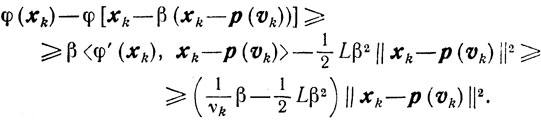(10.31)

Отсюда и из условия (10.29) получаем, что для любого β∈[0, 1] выполняется неравенство

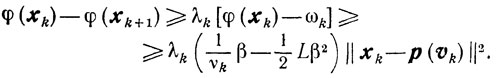(10.32)

В частности, выбирая

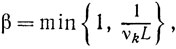
получаем при β = 1 (с учетом того, что в этом случае L≤1.ν_k)

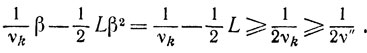
Если же

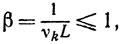
то

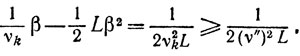
И окончательно приходим к неравенству

(10.33)

где

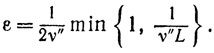
Из (10.33) и (10.26) получаем оценку (10.30).

Теперь обратимся к схемам метода проекций градиента.

Схема 1.

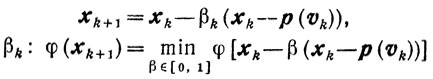(10.23)

и, кроме того, 0<ν'≤ν_k≤ν"<∞.

Сходимость. Если в условиях (10.27) -(10.29) положить y_k = p(v_k) и λ_k = 1, то мы приходим к схеме 1. В силу теоремы 10.3 из (10.30) получаем оценку

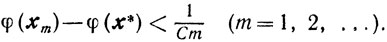
Устойчивость. Если вместо р(v_k) и β_k схеме найдены y_k и β_k, удовлетворяющие условиям (10.27) - (10.29), то в силу теоремы 10.3 справедлива оценка (10.30). И если все λ_k≥λ>0, то

Следовательно, в пределах изменения y_k и β_k, допускаемых условиями (10.28), (10.29), скорость сходимости остается того же порядка O(1/m), хотя множитель при 1/m - в оценке скорости сходимости увеличивается в у раз.

Схема 2.

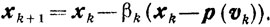(10.23)

В качестве β_k выбирается любое из чисел, удовлетворяющих условию

а величина ν_k может быть любой такой, что

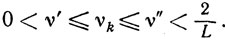
Сходимость. Из (10.31), учитывая условия, определяющие β_k и ν_k, получаем

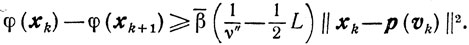
Оценка (10.26) приводит теперь нас к неравенству

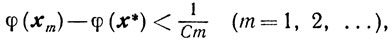
где

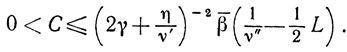
Устойчивость. Если при некотором β_k∈[β̄, 1] вместо p(v_k) найден элемент y_k, удовлетворяющий условию (10.29), то из (10.32) при λ_k≥λ>0 получаем

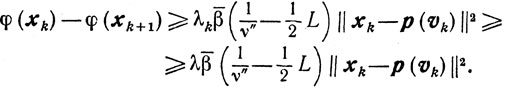
Оценка (10.26) приводит к неравенству

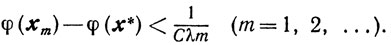
Таким образом, множитель при 1/m в этой оценке увеличивается в 1/λ раз по сравнению с предыдущим.

Обсуждение. Эта схема не требует затрат на одномерную минимизацию и при β_k=β̃∈[β̄, 1] представляет собой схему с постоянным шагом. В этом смысле она представляется весьма перспективной. Однако величина L-константа Липшица,- как правило, неизвестна, и сколько-нибудь удачно оценить ее в реальных ситуациях-задача настолько сложная, что обычно выбирают величину ν", намного меньшей предполагаемой величины 2/L, вследствие чего множитель 1/ν"-1/2 L в оценке величины С возрастет, существенно ухудшая априорную оценку скорости сходимости.

Схема 3. Здесь β_k = 1 (k = 0, 1, ...), а варьируется выбор ν_k на отрезке 0<ν'≤ν_k≤ν"<2/L:

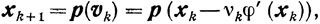
где р-оператор проектирования на множество X. Величина ν_k определяется соотношением

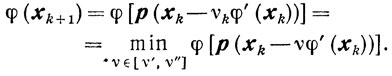
Сходимость. Из предлагаемого подхода к оценкам скорости сходимости следует, что эта схема представляет собой частный случай схемы 2 при β_k=1 и ν_k∈[ν', ν"]. Таким образом, оценка скорости сходимости здесь та же, что и в предыдущей схеме.

Устойчивость. Если вместо р(х_k-ν_kφ' (x_k)) вычислен элемент x̃_k+1 удовлетворяющий неравенствам

то так же, как и раньше, получаем, пользуясь тем, что x_k+1=p(ν_k) и β_k=1, оценку

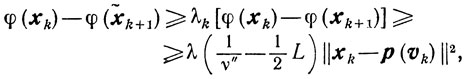
вследствие чего

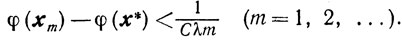
Обсуждение. Эту схему в смысле рассматриваемых априорных оценок скорости сходимости едва ли можно признать удачной: она не обладает преимуществами предыдущей схемы, поскольку требует проведения одномерной минимизации для определения величины ν_k и в то же время обладает худшей оценкой скорости сходимости по сравнению со схемой 1. Следует обратить внимание на оговорку: "в смысле рассматриваемых априорных оценок скорости сходимости". Эти слова означают, что при известных предположениях относительно исходной задачи скорость сходимости будет не хуже той, которую гарантируют наши оценки. И только. Но вполне возможно, что для конкретной задачи из рассматриваемого класса скорость сходимости может оказаться куда более высокой. Заметим, что все эти рассуждения предполагают некую идеализированную ситуацию в первую очередь в отношении точности вычислений, например, существование числа λ > 0, характеризующего эту точность.

Схема 4.

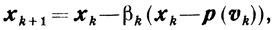(10.23)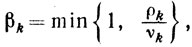

где

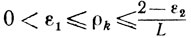
и

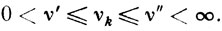
Сходимость. Из (10.31) получаем в результате элементарных выкладок, что

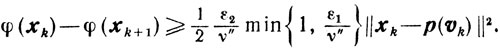
И неравенство (10.26) сразу приводит к оценке

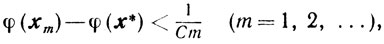
где

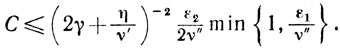
Устойчивость. Если вместо p(v_k) вычислена точка x̃_k+1 такая, что φ(x̃_k+1)≤(1-λ_k)φ(x_k)+λ_kφ(x_k+1), то, аналогично тому, как это делалось при анализе устойчивости предыдущей схемы, получаем, что в этом случае множитель при 1/m в оценке скорости сходимости возрастает в 1/λ раз.

Схема 5.

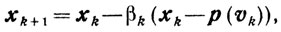(10.23)

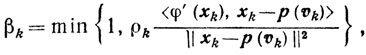(10.34)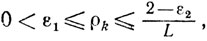

Сходимость. Из левой части (10.31) получаем при

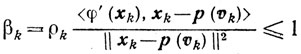
соотношение

(10.35)

И так как согласно (10.25)

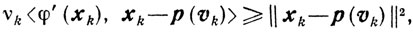
то, учитывая определение ρ_k, приходим к неравенству

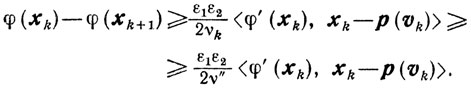
Если же β_k = 1, то

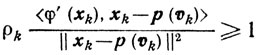
и, следовательно, из (10.31) получаем

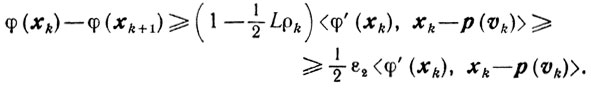
Выбирая

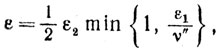
приходим к оценке

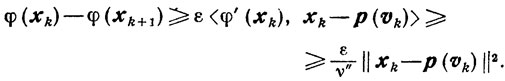(10.36)

Отсюда и из (10.26) приходим к той же самой оценке, что и в схеме 4.

Устойчивость. Здесь сохраняют силу те же соображения, что и в предыдущих двух схемах.

Схема 6.

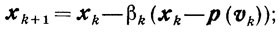(10.23)

в качестве β_k выбирается наибольшее из чисел, удовлетворяющих неравенствам

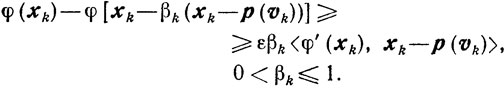(10.37)

Здесь число в может быть любым из интервала (0, 1): 0<ε<1, 0<ν≤ν_k≤ν"<∞.

Сходимость. Сначала покажем, .что существует β̄_k, удовлетворяющее условиям (10.37). Действительно, выбирая β̄_k по формуле (10.34), получаем из (10.35) и (10.36), что

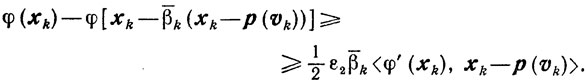
Но 0<ε₂<2, поэтому условия (10.37) выполняются.

Поскольку в,качестве β_k выбирается наибольшее из чисел, удовлетворяющих (10.37), то с учетом (10.25)

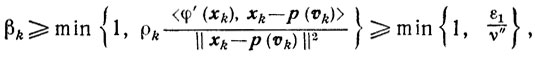
и, следовательно, справедлива та же оценка, что и в схемах 4 и 5.

Устойчивость. Если вместо p(v_k) вычислен y_k такой, что выполняется неравенство

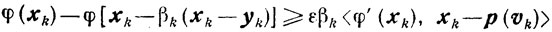
при некотором ε∈(0, 1], то ввиду того, что

получаем

Отсюда и из (10.26) получаем оценку

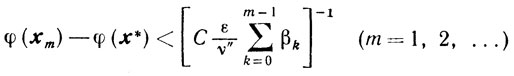
при

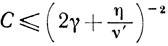
Если при этом 0<β̃≤β_k<1, то

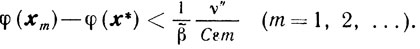
Обсуждение. Соображения о возможных преимуществах при отыскании β_k по этой схеме по сравнению со схемой 1 остаются теми же, что приводились при обсуждении схемы 2 метода градиентного спуска (см. п. 9.5).

Схема 7.

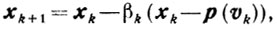(10.23)

а в качестве β_k выбирается наибольшее из чисел, удовлетворяющих неравенствам

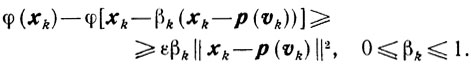(10.38)

Здесь число ε может быть любым из интервала (0, 1/ν"):

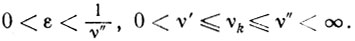
Сходимость и устойчивость. Из анализа сходимости предыдущей схемы ясно, что рд, определяемое формулой (10.34), удовлетворяет условиям (10.38). Таким образом, система (10.38) имеет решение. Доказательства сходимости и устойчивости здесь с очевидностью следуют из рассмотрений предыдущей схемы.

О контроле. Для того чтобы в процессе счета по методу проекции градиента контролировать сходимость релаксационного процесса, целесообразно на каждой итерации вычислять величину

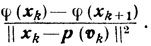
Оценка (10.26) показывает, что до тех пор, пока сохраняется ситуация

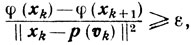
где величина ε определяется принятой точностью вычислений, процесс сходится со скоростью, порядок которой не ниже O(1/m).