10.3. Метод возможных направлений

Идея метода весьма прозрачна: среди всех возможных направлений в точке х_k выбирают то, вдоль которого функция убывает быстрей всего, и затем осуществляют спуск вдоль этого направления. Таким образом, метод возможных направлений можно рассматривать как естественное распространение метода градиентного спуска на задачи минимизации с ограничениями.

Напомним, что направление -s≠0 в точке х∈Х называют возможным, если существует такое число β̄>0 что x- βs∈X для всех β∈[0, β̄].

Мы уже говорили, что задача отыскания направления спуска в методах условного градиента и проекции градиента в случае, когда допустимое множество содержит нелинейные ограничения, является по сути дела задачей той же степени трудности, что и исходная. В отличие от этих методов, метод возможных направлений обладает тем преимуществом, что даже в случае нелинейных ограничений для отыскания направления спуска достаточно решить задачу линейного программирования либо простейшую задачу квадратичного программирования.

Итак, рассматривается задача

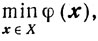
где

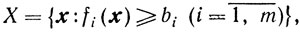
функции f_i(x) вогнуты и принадлежат классу С^1,1(Х). В общем случае в ограничениях, задающих множество X, различают две группы - линейные и нелинейные.

Для того чтобы при наших рассмотрениях выкладки были не слишком громоздкими, мы этого делать не будем. При этом появятся некоторые излишние требования относительно множества X, которые могут быть без труда сняты.

Условия существования возможных направлений. Пусть ε≥0 - произвольное число, вообще говоря, достаточно малое, о выборе которого речь пойдет при обсуждении алгоритма метода. Определим для x∈Х совокупность индексов

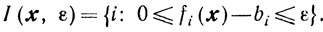
Заметим, что при ε = 0 будет

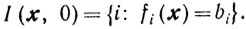
Рассмотрим в точке х ∈ X множества

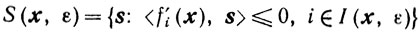
и

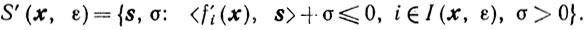
Установим условия существования возможного направления в точке х∈Х. В случае, когда х является внутренней точкой множества X, то есть I(x, 0) = ∅, любое направление - s в точке х является возможным. Предположим, что I (x, 0)≠∅.

Теорема 10.4.Для того чтобы направление - s было возможным в точке x∈Х, необходимо, чтобы s∈S(x, 0), и достаточно, чтобы s, σ∈S'(x,ε) хотя бы для одного ε≥0.

Необходимость. Пусть направление - s - возможное в точке х. Докажем, что s∈S(x, 0). Если это не так, то найдется такой номер i ∈ I (x, 0), что <f'_i(x), s> > 0. Из вогнутости функции f_i(x) следует для любого β > 0 неравенство

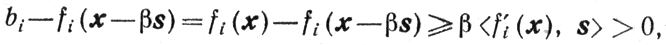
то есть х-βs∉X, что противоречит предположению о том, что направление -s-возможное.

Достаточность. Пусть s, σ∈S'(x, ε). Покажем, что направление -s-возможное. Если i∈I(x, ε), то есть f_i(x)-b_i>ε≥0, то малое перемещение из точки х по любому направлению и, в частности по направлению - s, не нарушит неравенства f_i(x)-b_i>0. Пусть i∈I(х, ε). Предположим, что для любого сколь угодно малого β>0 будет f_i(x-βs)<b_i, то есть направление - s не является возможным. Тогда, поскольку fi(x)^bh то для любого β> 0 будет

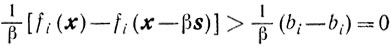
и, значит,

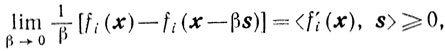
что противоречит условию s, σ∈S'(x, ε), так как σ > 0 и i∈I(х, ε).

Теорема доказана.

Поскольку в рассматриваемом методе направление спуска выбирается из множества S' (х, ε), то существенное значение приобретают условия не пустоты этого множества. Поскольку число ограничений исходной задачи конечно (равно m), то для любой точки x∈Х найдется число ε₀ = ε₀(x) такое, что для всех ε∈[0, ε₀] будет 1 (х, ε) = 1(х, 0). Вследствие этого достаточно рассмотреть критерий не пустоты множества S' (х, 0).

Теорема 10.5. Для того чтобы в любой граничной точке х∈Х было S' (х, 0)≠∅, необходимо и достаточно, чтобы множество X было регулярным^*. При этом существует такое σ₀ > 0, что S' (х, 0)≠∅ для всех σ∈(0, σ₀].

^* (Определение регулярности множества X см, в п. 3.3. )

Необходимость. Предположим, что нарушаются условия регулярности: для всех y∈Х найдется такой номер i, что f_i(y) = b;. Тогда для любого х∈Х будет i∈I (x, 0) и f_i(x - β(x-y)) = b_i для всех β∈(0, 1], поскольку х - β(x-y)∈Х. Вследствие этого

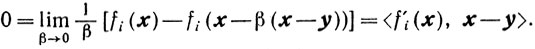
Так как направление -s=y-х - возможное в точке х, а точка у любая из X, то мы пришли к тому, что <f'_i(x), s> = 0 для любого возможного направления в точке X и следовательно S' (x, 0) = ∅, поскольку <f'_i(x), s>+σ>0, при σ>0 и i∈I(x, 0).

Достаточность. Пусть х - граничная точка множества X, то есть f_i(x) = b_i при некотором i∈I(x, 0). Из предположения регулярности множества X вытекает существование такого y∈Х, что f_i(y)>b_i для всех i = 1,...,m. Поскольку функции f;(x) вогнуты, то

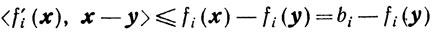
для i∈I(х, 0). Обозначим

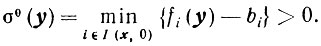
Тогда

для всех i∈I(x, 0). И так как направление - s = y - х возможное в точке х, то для всех i∈I(x, 0) будет

Пусть σ - любое такое, что 0<σ≤σ⁰(y). Тогда

и, значит, S'(x, 0)≠∅ для всех σ∈(0, σ⁰], где

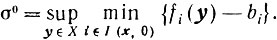
Задача выбора направления спуска. Пусть в результате k-й итерации вычислены х_k∈Х и ε_k > 0.

Рассмотрим задачу

при условиях

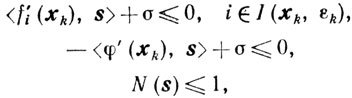(10.39)

где либо

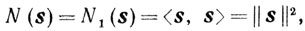(10.40)

либо

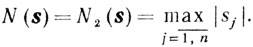
Обозначим через σ̃_k=σ̃(х_k) и s̃_k = s(x_k) решение задачи (10.39) и поясним эту задачу. Первое условие гарантирует, что направление - s̃_k - возможное. Второе условие обеспечивает максимальность величины <φ' (х_k), s>, то есть среди всех возможных направлений - s таких, что s, σ∈S' (х_k, ε_k), направление - s_k (при σ_k > 0) обеспечивает самое быстрое убывание функции φ(x). Наконец, третье условие избавляет от неограниченности решения задачи (10.39). Как уже говорилось, достоинством задачи (10.39) является ее относительная простота по сравнению с задачами выбора направления в предыдущих методах.

На следующей важной теореме базируются исследования сходимости метода возможных направлений.

Теорема 10.6.Для того чтобы точка х из регулярного множества X была оптимальной, необходимо и достаточно, чтобы для всех s и σ, удовлетворяющих условиям

было σ≤0.

Необходимость. Пусть х - точка минимума. Если найдется такая пара s, σ, удовлетворяющая условиям (10.42), (10.43), что σ>0, то s∈S'(х, 0) и, значит, направление-s -возможное (теорема 10.4) и, кроме того, <φ'(x), s> ≥ σ 0. Но по теореме 2.14, если х - точка минимума, то <φ' (х), s> ≤ 0 для всех возможных направлений. Противоречие.

Достаточность. Пусть для всех s и σ, удовлетворяющих условиям теоремы, будет σ≤0. Это условие формально запишем так:

Применим к системе (10.42)- (10.44) теорему 2.7 (Фаркаша): найдутся такие u_i≥0, i∈I(x, 0) и u₀ >0, что

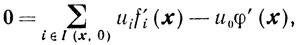(10.45)

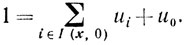(10.46)

Покажем, что предположение u₀ = 0 ведет к противоречию. В самом деле, из (10.46) в этом случае следует, что хотя бы одно u_l > 0 для l∈I (х, 0). Из регулярности X следует, что для всех l∈I (х, 0) существует z∈X такой, что f_i(z)>b_i. Тогда направление - s = z - x: будет возможным. Из вогнутости функции f_l(x) получаем

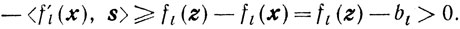
Умножим теперь равенство (10.45) скалярно на -5:

Так как -5 - возможное направление, то по теореме 10.4 s∈S(х, 0) и, следовательно, все слагаемые в правой части одного знака, а одно из них, а именно 1-е, заведомо отлично от нуля: - <f'_i(x), s> > 0, что противоречит равенству нулю всей суммы. Осталась единственная возможность: u₀ > 0. В этом случае условие (10.45) можно записать так:

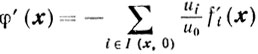
и, следовательно, по замечанию к теореме 3.4, точка х оптимальна.

Схемы метода. В качестве начального приближения х₀ выбирают любой элемент множества X, а ε₀ выбирают из полуинтервала (0, 1]. Пусть в результате k-и итерации вычислены x_k и ε_k. Опишем (k + 1)-ю итерацию.

Схема 1.

A. Решая задачу (10.39), вычисляют допустимые σ_k и s_k такие, что σ_k≥ξ_kσ̃_k, где 0ξ≤_k≤1.

B. Если σ_k≥_k, то, решая задачу одномерной минимизации, вычисляют β_k. При этом β_k должно удовлетворять условиям

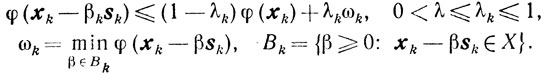(10.47)

Затем вычисляют х_k+1 = х_k-β_ks_k и полагают ε_k+1 = ε_k.

C. Если σ_k<ε_k, то полагают ε_k+1=δ_kε_k, где числа 6А должны удовлетворять условию 0<δ_k≤δ<1. И, наконец, полагают х_k+1 = х_k.

Обычно сходимость метода возможных направлений исследуется при условиях δ=1/2, λ_k = 1, ξ_k = 1. Однако при решении задачи (10.39) естественно возникают вычислительные погрешности, в результате которых вместо величины σ̃_k получают σ_k и соответствующий вектор s_k. Неравенства п. В, которым должна удовлетворять величина β_k, допускают, как это и было в ранее рассмотренных методах, погрешности в определении одномерного минимума функции φ(х_k - βs_k). Наконец, свобода выбора величин δ_k позволяет вносить элементы управления в процесс минимизации. В самом деле, если в процессе минимизации возникает ситуация п. С, то есть σ_k<s_k, то х_k+1 = х_k. Вполне возможен случай, когда медленное убывание величин ε_k приводит к тому, что для некоторого числа р будет

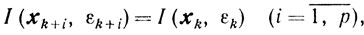
вследствие чего

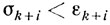
и

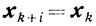
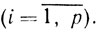
С другой стороны, известно, что быстрое убывание величины ε_k, особенно если точка x_k находится вне достаточно малой окрестности точки минимума, может привести к эффекту зигзагообразного движения около границы множества X, опять-таки существенно замедляющего сходимость процесса минимизации. Таким образом, в ходе накопления информации о сходимости процесса может возникнуть естественная необходимость изменения величин δ_k.

Схема 2.

A. Решая задачу (10.39), вычисляют допустимые σ_k и s_k такие, что σ_k≥ξ_kσ̃_k, где 0<ξ≤_k≤1.

B. Если σ_k<ε_k, то в качестве β_k выбирают наибольшее из чисел, удовлетворяющих условиям

для некоторого

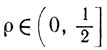
Затем вычисляют х_k+1 = x_k - β_ks_k и полагают ε_k+1 = ε_k.

C. Если _k<ε_k, то полагаютε_k+1 = δ_kε_k, где 0<δ_k≤δ<1. И, наконец, полагают х_k+1 = х_k.

Схема 3.

A. Решая задачу (10.39), вычисляют допустимые σ_k и s_k такие, что σ_k≥ξ_kσ̃_k, где 0<ξ≤ξ_k≤1.

B. Если σ_k≥ε_k, то выбирают

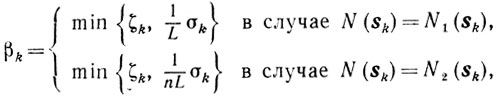(10.49)

где ζ_k = sup_β∈Bk β, a L - константа Липшица в условии φ(x)∈C^1,1(X). Затем вычисляют x_k+1 = x_k - β_ks_k и полагают ε_k+1 = ε_k.

C. Если σ_k<ε_k, то полагают ε_k+1 = δ_kε_k, где 0<δ_k≤δ<1. И, наконец, полагают х_k+1 = х_k.

Сходимость метода возможных направлений. Пусть -s - возможное направление в точке х∈Х. Рассмотрим множество

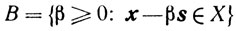
и определим величину ζ = sup_β∈B β. Таким образом, ζ характеризует наибольшее расстояние от точки х по направлению - s до границы множествах. Будем предполагать, что все f_i(x) принадлежат классу С^1,1(Х), то есть существование такой константы L₁ > 0, что для всех i = 1,..., m и любых х, y∈Х справедливо неравенство

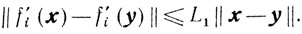
Обозначим

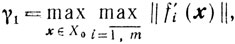
где множество

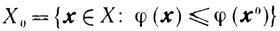
предполагается ограниченным.

Лемма 10.1.Для всех s таких, что s, σ∈S'(X, e) при х∈Х₀, ε>0 и N(s)≤1, справедливо неравенство

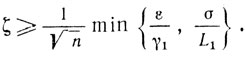(10.50)

Доказательство. Очевидно, что достаточно рассмотреть случай ζ<+∞. Обозначим y = х - ζs. Поскольку в нашем случае ζ = max_β∈B β, точка y является граничной и, значит, найдется такой номер I, что f_i(y)=b_i. Если в точке х будет f_i(x)-b_i>ε, то

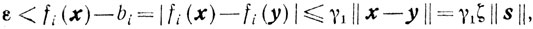
откуда

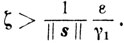
Если в точке х будет 0≤f_i(x) - b_i≤ε, то i∈I(x, ε), и поскольку s, σ∈S' (x, ε), имеем <f'_i(x), s>≤-σ. Воспользовавшись свойством вогнутости, получаем

или - ζ<f'_i(y), s>≤0. Так как s, σS'(x, ε), то направление - s - возможное и, следовательно, ζ > 0. Поэтому <f'_i (y), s> > 0. Наконец,

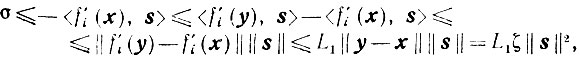
откуда

(10.52)

Пусть N (s) = N₁ (s) = ||s||²c≤c1. Тогда из (10.51) и (10.52) получаем

Пусть теперь N (s) = N₂ (s) = max_j=1,...,n |s_j|² ≤ 1. Так как N₁(s)≤n(N₂(s))², то из (10.51) получаем

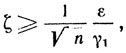
а из (10.52) получаем

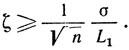
И окончательно

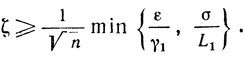
Таким образом, оценка (10.50) доказана для N (s) = N1 (s) и для N (s) = N₂(s).

Сходимость метода возможных направлений будем обосновывать при следующих предположениях:

1) выпуклая функция φ(х) принадлежит классу C^1,1(X)

2) вогнутые функции f_i(x) (i = 1,..., m) принадлежат классу С^1,1(Х);

3) множество X регулярно;

4) diam Х₀ = η<∞;

5) последовательность {x_k} строится по одной из трех схем.

Доказательство теоремы о сходимости состоит из пяти пунктов. В п. I оценивается снизу разность φ(х_k) - φ(х_k+1). В п. II доказывается сходимость последовательности {φ(x)}. В пп. III - V доказывается существование такой подпоследовательности {х_ki}, сходящейся к точке x̄∈Х, что σ̃_ki = σ̃(x_ki) стремится при i→∞ к σ̃(x̃), удовлетворяющему условиям теоремы 10.6, и тем самым доказывается оптимальность точки x̤̄: φ(x̄) = φ(x^*).

Теорема 10.7. Если выполняются условия 1)-5), то

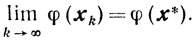
Если, кроме того, точка х^*-единственная, то

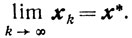
Доказательство. I. Покажем, что при σ_k>0 неравенство

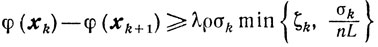(10.53)

справедливо для λ и ρ таких, что 0<ρ≤1/2 и 0<λ≤1. Действительно, в случае схемы 1 из леммы 9.3, условия (10.47) и условия <φ' (x_k), s_k> ≥ _k (последнее имеет место, поскольку s_k и σ_k допустимы для задачи (10.39)) получаем для любого β∈[0, ζ_k] неравенство

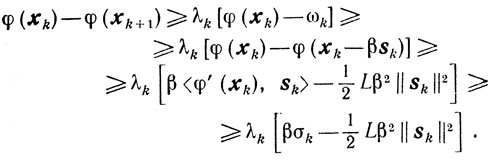(10.54)

Если

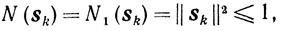
то для всех β∈[0, ζ_k] будет

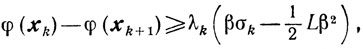
и при

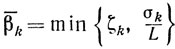
отсюда получаем неравенство

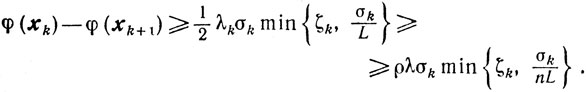
Если же

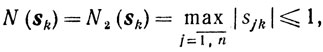
то поскольку N₁(s_k)≤n(N₂(s_k))², из (10.54) имеем

Отсюда при

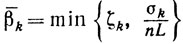
получаем неравенство

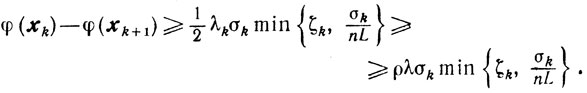
Итак, для схемы 1 неравенство (10.53) выполняется. Рассмотрим случай схемы 2. Из леммы 9.3 получаем

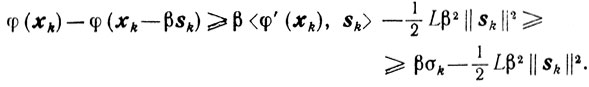
Отсюда при

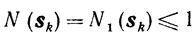
для

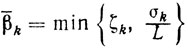
получаем

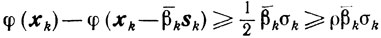
при

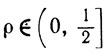
Это же неравенство справедливо при

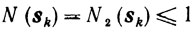
для

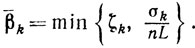
И поскольку

в качестве β_k в схеме 2 выбирают наибольшее из чисел, удовлетворяющих соотношению (10.48), то

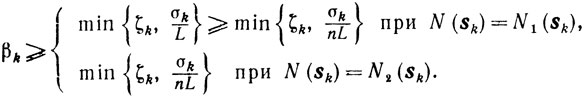
Отсюда и из (10.48) убеждаемся, что

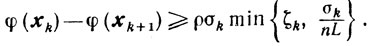
В случае схемы 3, поскольку β_k, найденное по формуле (10.49), таково, что _k = β̄_k, где β̄_k определяется так же, как и в предыдущих схемах, то оценка (10.53) справедлива при λ = 1 и ρ = 1/2 и, следовательно, при 0<λ≤1 и 0<ρ≤1/2.

II. Так как при σ_k<ε_k будет

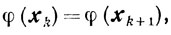
то отсюда и из (10.53) следует, что последовательность {φ(x_k)} монотонно убывает (точнее-не возрастает) и, кроме того, она ограничена снизу величиной

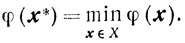
Вследствие этого, последовательность {φ(х_k)} сходится.

III. Докажем существование такой подпоследовательности {σ_kp}, что σ_kp→0 и ε_kp→0 при p→∞.

Заметим, что в задаче (10.39) пара σ = 0, s = 0 является допустимой и поэтому σ_k = max σ ≥ 0 (k = 0, 1,...).

Предположим, что найдется такое σ > 0, что все σ_k≥σ>0. Покажем, что тогда найдется такое ε > 0, что ε_k≥ε>0 (k = 0, 1, ...). Если ε_k→0 при k→∞, то найдется такой номер k₀ > 0, что 0<ε_k≤σ≤σ_k для всех k≥k₀. А по п. В любой из трех схем в этом случае ε_k = ε_k0 > 0 для всех k≥k₀. Противоречие.

Из (10.50) получаем неравенство

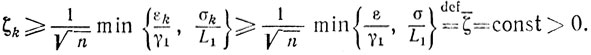
И поскольку в наших предположениях справедлива оценка (10.53), то мы приходим к неравенству

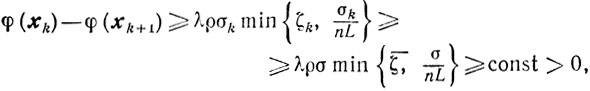
которое противоречит сходимости последовательности {φ(x_k)}.

Итак, существует подпоследовательность {σ_kp} такая, что σ_kp→0 при p→∞. Из пп. В и С всех трех схем следует, что ε_kp→0 при р→∞.

IV. Обозначим через σ̃'̃(х) решение задачи

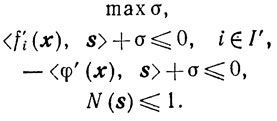(10.55)

Покажем, что σ̃'(х) непрерывно зависит от х.

В этой задаче I' - некоторая фиксированная совокупность индексов.

Для доказательства вначале заметим, что если σ^* и σ' таковы, что

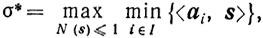(10.56)

a

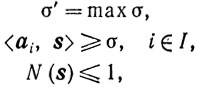(10.57)

то σ^* = σ'.

Действительно, пусть величине σ^* соответствует векторе s^*. Тогда для всех i∈I будет σ^*≤<a_i, s^*>, поскольку

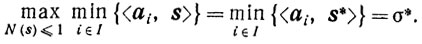
А значит, s^* удовлетворяет ограничениям задачи (10.57) и, следовательно, σ'≥σ^*. Пусть теперь величине σ' соответствует вектор s'. Тогда <a_i, s'> ≥ σ' для всех i∈I, то есть

и

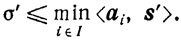
Но

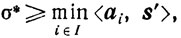
поэтому σ'≤σ^*. Окончательно получаем σ' = σ^*.

Вследствие этого σ̃' (x) - решение задачи (10.55) - таково, что

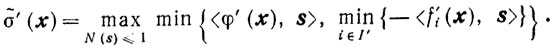
И так как непрерывны φ' (х) и все f'_i(x), то непрерывна и σ̃' (х). Для того чтобы в этом убедиться, достаточно доказать следующее утверждение: если функции ψ₁ (x, s) и ψ₂(x, s) непрерывны по совокупности переменных х и s, то непрерывна и функция

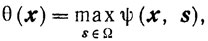
где

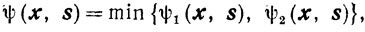
a Ω - компакт.

Чтобы доказать непрерывность θ(x) сначала покажем, что ψ(x, s) непрерывна по совокупности переменах х и s.

Пусть в точке (x̄, s̄) будет

например,

Тогда для всех (х, s) из достаточно малой окрестности точки (х̄, s̄) будет

то есть ψ(x, s) = ψ₁(x, s), и, следовательно, ψ(х, s) непрерывна в точке (х, s). Пусть теперь

Тогда

при (x, s)→(x̄, s̄) ввиду непрерывности ψ₁(x, s) и ψ₂(x, s).

Покажем непрерывность θ(x) в точке x̄. Для этого введем множество

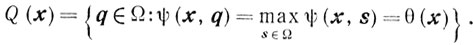
Возьмем произвольную последовательность

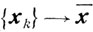
и рассмотрим последовательность {q_k}, q_k∈Q(x_k), сходящуюся к q̄. Тогда

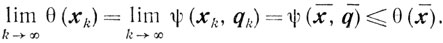
С другой стороны, пусть q̄̄∈Q(x̄). Тогда

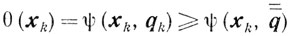
при всех k = 1, 2,.... При k→∞ отсюда имеем

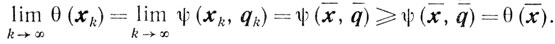
Сравнивая с неравенством

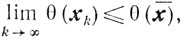
заключаем, что

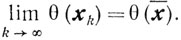
Непрерывность доказана.

По индукции теперь легко доказать непрерывность:

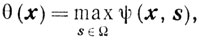
где

а функции ψ_i(x, s) непрерывны по совокупности переменных x, s. Значит, непрерывна и σ̃' (х), поскольку непрерывны по совокупности переменных все скалярные произведения <φ'(x), s> и <f'_i(x), s>.

V. Докажем существование подпоследовательности {x_kp}, сходящейся при p→∞ к такому x̄, которому соответствует σ̃(x̄)=0 -решение задачи

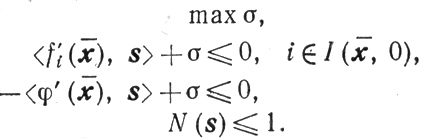
Тем самым в силу теоремы 10.6 будет доказана оптимальность точки х̄. Ввиду непрерывности функции φ(х) отсюда следует, что

А поскольку последовательность {φ(х_k)}- сходящаяся, то тем самым будет доказано, что

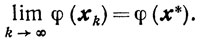
Из п. III следует, что σ_kp→0 при p→∞. Чтобы обозначения не были громоздкими, будем полагать, что σ_k→∞ при k→∞. Из приведенных выше рассуждений ясно, что это допущение не умалит общности доказательства.

Последовательности {σ_k} соответствует последовательность {x_k}, все элементы которой ввиду п. I принадлежат ограниченному множеству

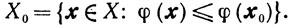
Выберем из {x_k} сходящуюся подпоследовательность. Не меняя обозначений, будем полагать, что lim_k→∞ х_k = х. Так как число ограничений исходной задачи конечно (равно m), то конечно и число различных наборов I(x_k, ε_k), поэтому существует такой набор I', который остается неизменным для бесконечного числа элементов из {х_k}. Опять-таки, не меняя обозначений, будем полагать, что всем {х_k} соответствует набор I'. Итак, x_k→x̄ и I (х_k, ε_k) = I', σ_k→0 при k→∞. В силу п. А всех трех схем σ_k≥ξ_kσ̃_k≥ξσ̃_k поэтому lim_k→∞ σ̃_k = 0. С другой стороны, σ̃_k = σ̃' (x_k) → σ̃'(х̄) согласно п. IV. Так что σ̃' (х) = 0. Далее, из того, что I' = I(х_k, _k), следует 0≤f_i(x_k)-b_i≤ε_k. Для всех i∈I' (k = 0, 1, ...). Но ε_k→0, x_k→x̄, поэтому i∈I(x̄, 0) при всех k≥k₀. Значит, I' = I (х_k, ε_k)⊆I(х̄, 0) при всех k≥k₀. Тогда σ̃(x̄)≤σ̃'(x̄), где σ̃(х̄) есть максимум о в задаче (10.55) при замене I' на I (х̄, 0) и х на х̄, а σ̃' (х) есть максимум а в задаче (10.55) при x = x̄. Поскольку было показано σ̃'(x̄)=0, то а σ̃(x̄)=0. В силу теоремы 10.6 это означает оптимальность точки х̄.

Таким образом доказано, что любая предельная точка последовательности {х_k} является оптимальной. Отсюда следует

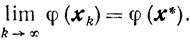
Очевидно, что в случае единственности оптимальной точки х^* вся последовательность {х_k}→x^*. Теорема 10.7 доказана.

Замечание 1. Все три схемы сконструированы таким образом, что из доказанной нами теоремы следует устойчивость метода возможных направлений к возможным вычислительным ошибкам при реализации п.п. А, В и С всех трех схем.

Замечание 2. Проблема оценки скорости сходимости метода возможных направлений при весьма общих предположениях о задаче выпуклого программирования до последнего времени остается нерешенной.

Случай присутствия линейных ограничений. Если некоторые ограничения, определяющие множество X, линейны, то целесообразно разбить ограничения на две группы-линейные и нелинейные:

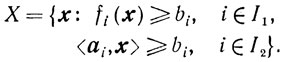(10.58)

В этом случае задача выбора направления спуска приобретает следующий вид:

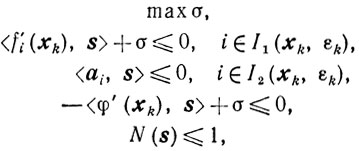(10.59)

где

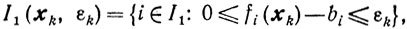
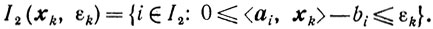
Естественно, что все три схемы метода в этом случае остаются прежними. Остаются прежними и все рассуждения при доказательстве сходимости метода. При этом требование регулярности в нашем случае можно ослабить по сравнению с тем, которое было введено раньше. А именно, множество X, определенное соотношениями (10.58), будем называть регулярным, если для всех i∈I₁ найдется такой х∈Х, что f_i(x)>b_i(i∈I). Таким образом, свойство регулярности относится лишь к нелинейным ограничениям.

О решении задачи выбора направления. В случае, когда

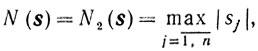
задача выбора направления (10.59) является задачей линейного программирования и, следовательно, для ее решения применимы конечные алгоритмы. Если же N(s) = N¹(s) = ||s||², то задача (10.59) имеет нелинейное ограничение. Покажем, что эта задача в определенном смысле эквивалентна задаче квадратичного программирования специального вида.

Запишем задачу (10.39) следующим образом:

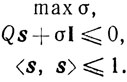(10.60)

Здесь Q - матрица, строками которой являются век-горы [f'_i(x)]^T при i∈I(x, ε) и [-φ'(х)]^Т. Во избежание громоздкости, индекс k - номера итерации - здесь опущен. Через I обозначен вектор I^T = (1, 1, ..., 1).

Заметим, что поскольку σ = 0, s = 0 является допустимой парой, а допустимое множество задачи (10.60) ограничено и замкнуто, то эта задача всегда разрешима. Рассмотрим задачу

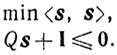(10.61)

Очевидно, что если множество

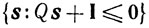
не пусто, то решение этой задачи существует. Обозначим его через s₁. Заметим, что s₁≠0, так как s = 0 не является допустимой точкой задачи.

Теорема 10.8.

1) Пара

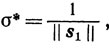
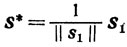
является решением задачи (10.60).

2) Если множество

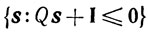
пусто, то оптимальное значение а в задаче (10.60) равно нулю.

Доказательство. Так как

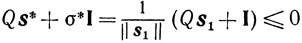
и

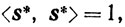
то пара σ^*, s^* допустима для задачи (10.60). Предположим, что найдется пара σ̄, s̄, удовлетворяющая ограничениям задачи (10.60), такая, что σ̄>σ^*>0. Тогда точка 1/σ̄ s̄ будет допустимой для задачи (10.61): а

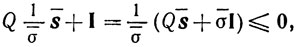
и поэтому

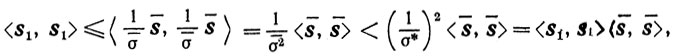
откуда получаем неравенство <s̄, s̄> > 1, противоречащее допустимости точки s̄ для (10.60). Вторая часть теоремы является очевидным следствием ее первой части. Для решения задачи (10.61) существуют конечные алгоритмы, тщательное изложение которых читатель в случае необходимости может найти в [7], [13].