10.4. Метод случайного поиска

Как мы видели, в задачах минимизации с ограничениями-собственно задачах математического программирования - задача выбора направления спуска обладает в общем случае задания множества X большой трудоемкостью, которая зачастую делает изложенные методы минимизации малоэффективными. Исключение составляют случаи, когда множество обладает простой геометрической структурой (например, является многомерным параллелепипедом), но нас интересует именно общий случай. В этой ситуации может оказаться весьма перспективным метод случайного поиска - когда направление спуска выбирается случайным образом. Естественно, что при этом мы, вообще говоря, будем существенно проигрывать в скорости сходимости, однако простота выбора направления может компенсировать эти потери с точки зрения общих затрат труда на решение задачи минимизации.

Итак, рассматривается задача минимизации функции φ(x) на множестве X. Будем предполагать, что найдена точка x_k∈X.

Выбор направления спуска. На n-мерной единичной сфере с центром в начале координат выбирается случайная точка r_k, подчиняющаяся на этой сфере равномерному распределению, и затем направление спуска - s_k выбирают из условий s_k = θ_kr_k, где

Схема 1. В качестве начального приближения х₀ выбирают любую точку х₀∈Х. По вычисленной на k-й итерации точке x_k строят (k+1)-ю точку x_k+1 по формуле

качестве β_k выбирается любое число из

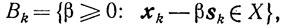
удовлетворяющее неравенству

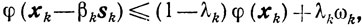(10.47)

где λ_k любое такое, что 0<λ≤λ_k≤1, а

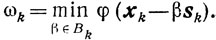
Схема 2.

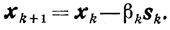
В качестве β_k выбирают наибольшее из чисел, удовлетворяющих условиям

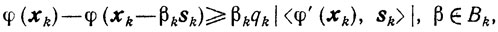(10.64)

где числа q_k любые такие, что

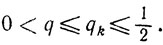
Сходимость. Доказательство сходимости будем проводить в следующих предположениях:

1) множество X выпукло и замкнуто;

2) множество X регулярно, то есть в Е_n существует сфера радиуса ρ>0, целиком принадлежащая множеству X;

3) для любого элемента х₀∈X множество

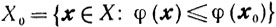
ограничено;

4) функция φ(х) выпукла и φ(x)∈C^1,1(X).

Замечание. Нетрудно убедится, что условие регулярности 2) эквивалентно условию регулярности, введенному в гл. 3, п. 3.1.

Для обоснования сходимости процедуры случайного поиска необходимо рассмотреть ряд свойств.

Свойство А. Если точка х̄∈X не является оптимальной, то найдется такой ȳ∈Х, для которого справедливо неравенство

Доказательство. Пусть y является проекцией точки z = x̄ - φ' (x̄) на множество X. В силу свойств проектирования имеет место соотношение

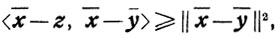
то есть

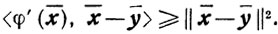
Отсюда и следует свойство А, поскольку равенство х̄=ȳ является необходимым и достаточным условием оптимальности х̄ (теорема 2.16).

Всюду ниже через х̄ и ȳ обозначены точки, удовлетворяющие свойству А.

Свойство В.Найдется такое число δ>0, что множества

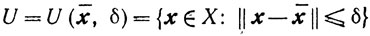
и ' .

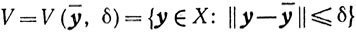
не пересекаются, и существуют такие n-мерные сферы R₁ и R₂ радиусов ρ₁ и ρ₂, что R₁⊂U и R₂⊂V.

Доказательство вытекает из свойства А (так как x̄≠ȳ) и предположений 1) и 2)^*.

Свойство С. Для ξ=<φ'(x̄), x̄-ȳ> > 0 найдется такое δ>0, что для всех x∈U (х̄, δ) и y∈V(ȳ, δ ) будет выполняться неравенство

Доказательство. Обозначим

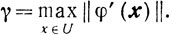
Предположение 4) гарантирует, что γ<+∞. Выберем

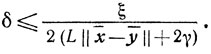
Пусть u = х-х̄ и v = y-ȳ (x∈U, y∈V), тогда

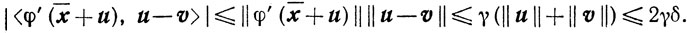
Далее,

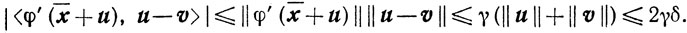
^* (Легко показать, что если точка w-центр сферы R (радиуса ρ), принадлежащей регулярному множеству X, то можно взять

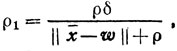
причем центром сферы R₁ будет точка

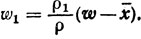
Аналогично и для R₂.)

Но ввиду предположения 4) и свойства А получаем

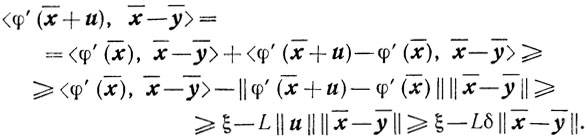
Три последних соотношения и выбор величины δ доказывают справедливость свойства С.

Определение. Мы скажем, что осуществилось событие M=M(х, s), если найдется такое β̃>0, что y = х-β̃s∈V (у, б), где x∈U (x̄, δ), а-s-возможное направление, выбранное методом случайного поиска.

Свойство D. Если наступает событие M_k = M(х_k, s_k), то существует такое ε>0, что

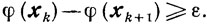
Доказательство. 1) Случай схемы 1. Пусть x_k∈U', а y_k-любая точка из пересечения луча x_k-βs_k с множеством V. Так как

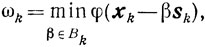
то для всех β∈ [0,1] справедливо неравенство

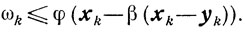
Отсюда, из (10.47) и из леммы 9.3 получаем неравенство

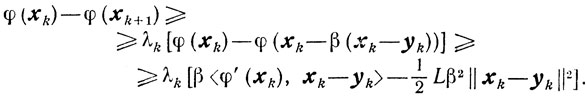
Но

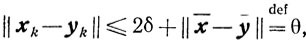
поэтому из свойства С получаем, что для всех β ∈ [0,1] будет

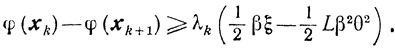
Пусть

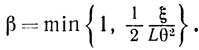
Если β = 1, то Lθ²≤1/2ξ и

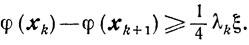
Если

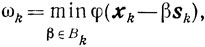
то

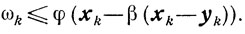
так как λ_k≥λ>0, то при

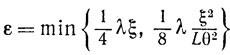
свойство D становится справедливым.

2) Случай схемы 2. Из свойства С следует, что

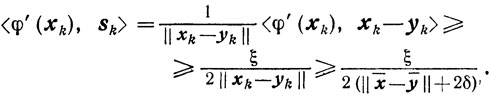(10.65)

Теперь убедимся, что

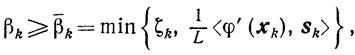(10.66)

где

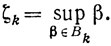
Так как

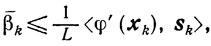
из леммы 9.3 следует неравенство

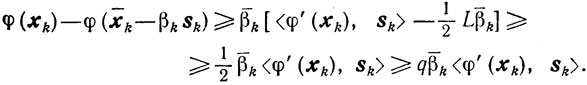
Таким образом, β̄_k удовлетворяет соотношениям (10.64). поскольку в качестве β_k выбирают наибольшее из чисел, удовлетворяющих условиям (10.64), то справедливо неравенство (10.66).

Выберем величину δ>0 столь малой, что ||х̄-ȳ|| - 2δ > 0. Так как

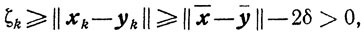
то из (10.66) и (10.65) следует, что

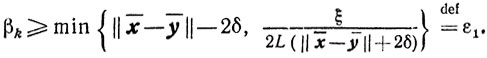
Отсюда и из (10.64) и (10.65) получаем

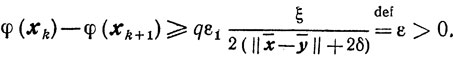
Свойство Е. Если последовательность {х_k} такова, что x_k∈U, то

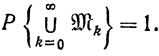
Доказательство. Из свойств А и В следует, что

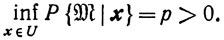
При фиксированных x₀, x₁ ... соответствующие события M₀, M₁ ... взаимно независимы, так как взаимно независимы случайные величины s₀, s₁ .... Следовательно,

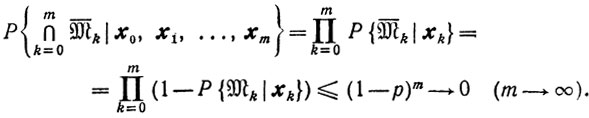
Здесь M̄_k означает событие, дополнительное к событию M_k, то есть M̄_k означает, что событие M_k не происходит. Поэтому согласно закону "нуля или единицы"

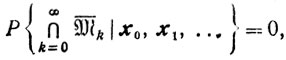
то есть

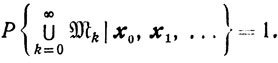
Это и означает, что

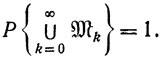
Теорема 10.9.

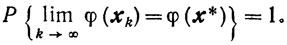
Доказательство. В силу предложенной процедуры, последовательность случайных величин {φ(х_k)} монотонна:

ограничена:

следовательно, существует

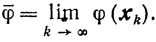
значит, с вероятностью, равной единице, найдется такой номер k₀, что для всех k=k₀+1, k₀+2, ... будет выполняться неравенство

Если для любого, сколь угодно малого δ₁>0 найдется такая подпоследовательность {x_ki}, что

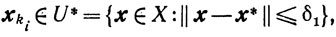
с вероятностью, равной единице,

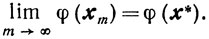
Предположим, что существует такое число δ₁>0, что окрестность U* попадает лишь конечное число точек последовательности {x_k}. Не ограничивая общности, можно полагать, что все x_k∈U*. Тогда с вероятностью, равной, единице, найдется такой случайный номер k≥k₀, что осуществится событие M_k, а следовательно, будет

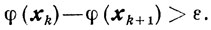
Это противоречит условию (10.67). Теорема доказана.