10.5. Метод проектирования случайного направления

Изложенный в предыдущем разделе метод минимизации может оказаться неэффективным. Дело в следующем. С ростом числа n - размерности пространства E_n - убывает вероятность того, что направление r_k является возможным. Скорость этого убывания характеризует простой пример, когда

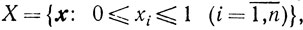
a точка х_k = 0. В этом случае вероятность того, что случайное направление r_k будет возможным, очевидно, равна 2^-n". Поэтому для получения возможного направления требуется при больших n на каждой итерации, вообще говоря, большое число испытаний, причем каждое испытание связано с проверкой, будет ли для достаточно малого β точка х_k-βr_k принадлежать множеству X, то есть будет ли r_k = s_k и, следовательно, с определенными вычислениями.

В методе, которому посвящен настоящий раздел, случайное направление становится возможным в результате проектирования на допустимое множество.

Обозначим через z_k проекцию точки х_k-Δ_kr_k на множество X. Здесь Δ_k = sign <φ' (х_k), r_k>, а r_k строится так же, как и в предыдущем методе.

Схема 1.

В качестве β_k выбирают любое из чисел, удовлетворяющих условиям

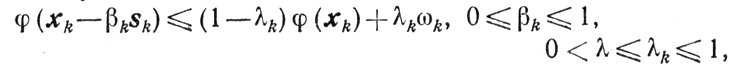
где

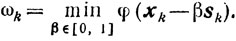
Схема 2.

качестве β_k выбирают наибольшее из чисел, удовлетворяющих условиям

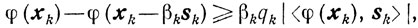
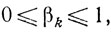
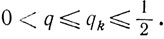
Для обоснования сходимости метода проектирования применима та же методика, что и в предыдущем разделе. 1 При этом требование регулярности множества X становится излишним.

В самом деле, рассмотрим множество^*

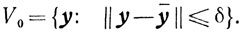
Заметим, что

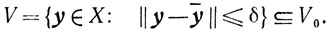
^* (Здесь ȳ, U и V те же, что в п. 10.5.)

Будем говорить, что осуществилось событие N = N(х, r), если найдется такое α>0, что х-αr∈V₀, где х∈U, а r -направление, выбранное методом случайного поиска. Определение события M = M(х, s) остается прежним, но при этом

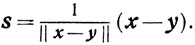
Свойство F.Если осуществилось событие N_k = N(x_k, r_k), то осуществится и событие M_k = M (х_k, s_k).

Доказательство. Пусть v_k = x_k-αr_k∈V₀, a y_k-ее проекция на множество X. Из свойств проекции следует, что

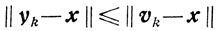
и любом x∈Х и, в частности,

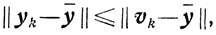
есть y_k∈V.

Наконец, очевидно, что для всех x∈U будет

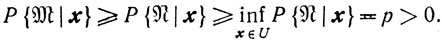
Обосновать сходимость процесса минимизации теперь не представляет труда, если повторить рассуждения, которые использовались при доказательстве теоремы 10.9.