4.2. Планирование и эвристический поиск

Независимо от того, пытаемся ли мы найти последовательность шахматных ходов, позволяющих нам выиграть партию,, нащупать ход рассуждений, который приведет нас от аксиом к доказательству некоторой теоремы евклидовой геометрии, или выяснить кратчайший путь со службы на званый вечер, мы можем представлять себе дело так, как будто мы ведем поиск в некотором обширном пространстве состояний. Мы располагаем множеством всевозможных позиций на шахматной доске, списком уже доказанных теорем евклидовой геометрии или перечнем всех улиц и переулков в городе и его пригородах для нашей задачи о маршруте. Кроме того, у нас есть набор операторов, переводящих нас из одного состояния в другое: правила игры в шахматы, правила дедуктивного вывода в геометрии или движение по прямой и повороты на перекрестках в последней задаче. В каждом случае мы начинаем с некоторого начального состояния и приходим к решению задачи, если нам удается найти последовательность шагов - операций, которые приведут нас в приемлемое конечное состояние. Более того, часто нам хотелось бы, чтобы и сама последовательность таких шагов была оптимальной в некотором смысле, как это имеет место в задаче о маршруте, когда нам хочется по возможности быстрее попасть на ужин.

В случае доказательства теорем планирование и действие неразличимы. Но при игре в шахматы мы должны планировать на несколько ходов вперед, ведь мы не можем забрать назад уже сделанный ход, столкнувшись с совершенно неожиданным и губительным для нас ответным ходом противника. И конечно, если мы спешим в гости, нет смысла попробовать сначала проехать часть каждого из нескольких возможных путей, с тем чтобы выяснить, какой из них короче. (Последний пример напоминает нам о необходимости компромиссов в процессе обучения: иногда полезно заняться экспериментированием, чтобы собрать информацию, которая окажется полезной в дальнейшем, хотя используемый при этом "путь" будет, без сомнения, далек от оптимального.) Таким образом, разумная система должна не просто двигаться в пространстве состояний, определяемом (или определяющем) решаемой в данный момент проблемой; она должна, кроме того, уметь построить модель, описывающую некоторые участки этого пространства, и с помощью этой модели исследовать различные возможные планы действия, прежде чем выбрать один из них.

Для того чтобы представить себе эту ситуацию несколько более конкретно, будем считать, что в распоряжении шофера имеется некая модель в виде карты, изображенной на рис. 52, и что для упрощения рассуждении расстояния на карте действительно пропорциональны протяженности соответствующих участков дороги.

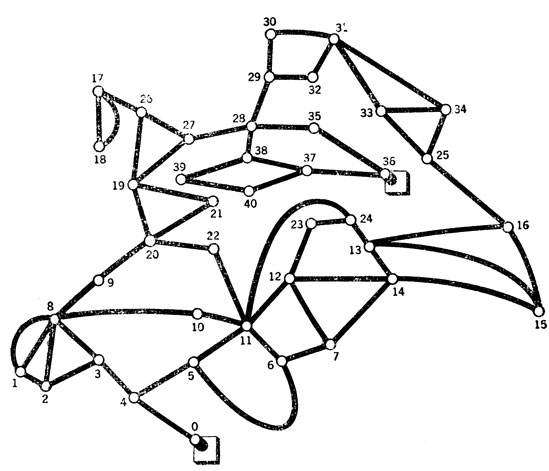
Рис. 52. Как найти кратчайший путь со службы (пункт 0) в гости (пункт 36) - задача, рассматриваемая на рис. 53-59. На этой карте расстояния между пунктами пропорциональны истинным расстояниям между перекрестками

Какой же путь от работы в гости самый короткий? Пусть читатель попробует выяснить это, а затем подробно объяснит, что он для этого делал. При этом может оказаться, что, имея возможность видеть всю карту в целом, вы воспользуетесь какими-то геометрическими соображениями. Мы же попробуем сейчас показать, как это можно сделать, пользуясь локальным, пошаговым алгоритмом.

Прежде чем описать несколько алгоритмов, помогающих на стадии планирования найти подходящий путь на графе, который служит моделью пространства состояний с определенными на нем операциями, нам хотелось бы высказать несколько общих соображений.

1. Во многих случаях нельзя рассчитывать на получение подробной карты, с тем чтобы на каждом перекрестке "с одного взгляда" было ясно, куда надо повернуть -направо или налево. Вместо этого, как при игре в шахматы, у нас есть возможность генерировать по описанию одного состояния описания всех тех состояний, в которые можно попасть за один ход. В действительности для большинства реальных ситуаций число возможных состояний превышает объем памяти самых современных и самых больших машин, и поэтому мы можем хранить в явном виде лишь те состояния, которые либо потенциально важны для решения текущей задачи, либо настолько важны для решения других задач, что их стоит запомнить на будущее. Последнее соображение особенно важно при обучении (шашечный автомат Сэмюэла хранит в своей памяти гроссмейстерские партии, к которым он время от времени обращается), но мы не будем касаться этого вопроса здесь.

2. Одно из следствий замечания о размерах пространства состояний заключается в том, что мы практически никогда не можем пойти по пути полного перебора возможностей, а должны каким-то образом (это целое искусство, о котором мы еще поговорим) ограничивать свой поиск правдоподобными альтернативами. Однако такое выделение правдоподобных альтернатив обычно опирается на надежную информацию. Например, если в нашем примере с рис. 52 речь идет о банкете в городской ратуше, то разумно предположить, что на каждом перекрестке будут дорожные знаки, показывающие, как проехать на главную площадь города, и, следовательно, ни в каком поиске на стадии планирования нет нужды. Но если вы собрались в гости к приятелю, живущему на окраине, то вся информация, на которую вы можете рассчитывать, оказавшись у перекрестка, ограничивается смутным ощущением, что "эта улица, кажется, ведет в нужном направлении".

3. Игра в шахматы связана с дополнительными осложнениями, которых мы касаться не будем ввиду нашей приверженности к задаче о выборе маршрута. В шахматах мы стараемся найти ход, не только непосредственно приводящий нас к выгодной позиции, но и минимизирующий опустошение, которое может вызвать умный противник своим ответным ходом.

4. Возможно, нам удастся воспользоваться специальными знаниями для того, чтобы "сократить" граф состояний, объединив некоторые его узлы в один, и тем самым уменьшить числа альтернатив, которые надо рассматривать. Например, если мы знаем, что самый быстрый путь в гости частично проходит по магистральному шоссе, то мы можем убрать с графа все развязки, кроме тех, по которым мы собираемся на него выехать и с него съехать, и оставить на карте только тот кусок графа, который соответствует улицам пригорода, где живет наш друг^*.

^* (Такая операция эквивалентна объединению всех выброшенных верши" в одну, соединенную только с нулевой вершиной. - Прим. перев.)

5. Один из полезных методов поиска оптимального пути использует "двусторонний поиск". Некоторые из читателей наверняка признаются, что искали оптимальный путь на рис. 52, "формируя" маршрут с двух разных концов - и от службы, и от пункта назначения. Можно вспомнить также, насколько удобно решать задачи по математике, отталкиваясь не только от их условий, но и от ответа (если он приведен), подсказывающего иногда, в каком направлении искать решение. Здесь мы рассмотрим лишь "однонаправленные" методы поиска, идущие от начального состояния, хотя на самом деле существует и их двусторонние аналоги.

Обратимся теперь к некоторым подходам, помогающим нам избегать необходимости рассматривать на стадии планирования все возможные траектории, получающиеся на модели. Множество альтернативных маршрутов на рис. 52 можно изобразить с помощью дерева (рис. 53), корень которого соответствует исходному пункту 0, а из каждой вершины выходит столько Дуг, сколько путей на рис. 52 выходят из соответствующего пункта, не считая того пути, по которому, мы в этот пункт попали. Несколько первых уровней такого дерева, отвечающего Рис. 52, приведено на рис. 53. Во время наших дальнейших рассуждений мы просили бы читателя постоянно возвращаться к рис. 52 для проверки, соглашается ли он с оценками расстояний, которыми мы пользуемся для отбора и отбрасывания вершин на этом дереве решений. Эти оценки не всегда будут верны, так что это - настоящее упражнение на понимание основных принципов.

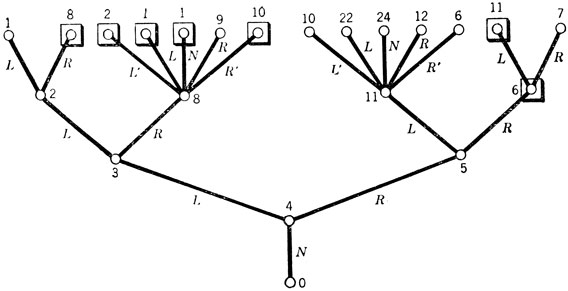
Рис. 53. Первые пять уровней 'дерева решений' для задачи, представленной на рис. 52. От каждой вершины отходят 'ветви' к вершинам, отвечающим всем тем пунктам, в которые можно попасть по путям, показанным на рис. 52, не проезжая каких-либо промежуточных пунктов. Это дерево можно 'подстричь', отбрасывая вершины, окруженные квадратиками, как только мы находим более короткий путь к пункту с тем же номером. Например, на рис. 52 в пункт 8 ведут два пути: один, проходящий через пункты 4 и 3, и другой, более длинный, проходящий через пункты 4, 3 и 2; соответствующая этому последнему вершина заключена в квадратик. Говоря о длине пути, мы имеем в виду расстояние по настоящей карте (рис. 52), а не по дереву решений, что становится понятным если рассмотреть пути, ведущие в пункт 6

И хотя на этом рисунке показано всего пять ярусов, уже сейчас видно, что дерево можно "подстричь". Например, на рис. 53 есть три вершины, соответствующие пункту 1 на рис. 52, и ясно, что если путь в гости лежит через пункт 1, то отрезок пути от работы к пункту 1 в свою очередь должен быть наикратчайшим. Поэтому на рис. 53 можно "обрезать" все ветви, проходящие через вершину 1 и идущие вначале по пути NLRL и NLRN, поскольку оба эти начальных пути длиннее, чем путь NLLL, тоже ведущий в пункт У. Аналогичным образом отбрасывается вершина 6, к которой ведет путь NRR, и все остальные вершины, заключенные в квадратики.

Особенно важно сейчас отметить, что отброшенный путь к вершине 6 является первым - подчеркиваю первым, а не вторым - с которого мы начали. Это получилось потому, что путь с двумя перекрестками (4 и 5) оказался длиннее, чем с тремя (4, 5 и 11), хотя мы обратились к последней возможности позже из-за лишнего перекрестка. В подобном случае нам приходится отбрасывать все ветви, выращенные из старого узла, и начинать анализировать ветви, являющиеся продолжением только что найденного более короткого пути, поскольку кратчайший путь, если он только проходит через вершину 6, просто не может начинаться с неэффективного начального пути в 6.

Этот метод, известный в теории управления как метод динамического программирования ("Если путь из a в c через b оптимален, то оптимальными должны быть и оба отрезка из a в b и из b в c"), несомненно, позволяет сократить число ветвей, которые нужно выращивать на нашем дереве решений, и в конечном счете обязательно приводит к решению, поскольку по сути дела мы при этом вовсе не отказываемся от полного перебора, а не рассматриваем лишь те пути, неэффективность начальных отрезков которых сразу указывает, что они не могут служить кратчайшим путем куда бы то ни было. А последние слова "куда бы то ни было" вскрывают самую сущность того, почему этот метод поиска почти наверняка потребует гораздо больше времени, чем тот, которым воспользовался читатель, решая задачу о кратчайшем маршруте на рис. 52; этот метод не использует информации о желанной цели.

Для того чтобы понять, как можно использовать информацию о цели, нам придется вернуться к проблеме полной и неполной информации, затронутой в пункте 2. Если имеющаяся информация полна и совершенно надежна, то построенное дерево решений в конечном счете "сведется" к оптимальному решению без каких-либо лишних ветвлений.

Один из видов представления полной информации - а мы еще раз подчеркиваем, что на стадии планирования такой информации обычно нет, - состоит в том, что для каждого узла x приведенного графа будет указана протяженность h(x) кратчайшего пути из x в цель. В этом случае па каждом перекрестке мы практически сразу смогли бы решить, в какую сторону теперь двигаться, так же как если бы мы следовали дорожным знакам, ведущим к ратуше.

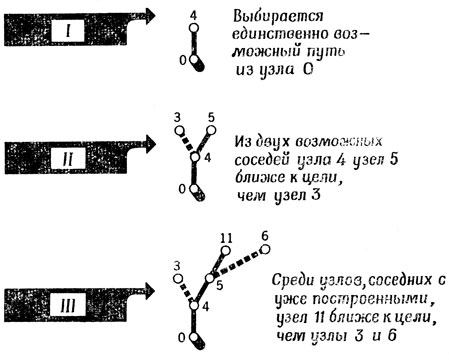
Рис. 54. Применение эвристики Дорана - Мичи для исследования карты, изображенной на рис. 52. Читателю предлагается самому проверить, не сделали ли мы каких-нибудь ошибок. Для этого полезно иметь циркуль и с его помощью проверять расстояния по рис. 52. Показаны первые три этапа исследования (I-III). Пунктиром показаны возможные пути, которые еще предстоит исследовать и которые исходят из уже построенных узлов. Сплошные же линии соединяют старый узел с новым, построечным по принципу 'ближайшего узла по прямой'

Именно на этом соображении основан подход, предложенный Дораном и Мичи [60] в схеме, которую они назвали методом градиента, но только вместо истинного расстояния h(x) они использовали нечто, что называлось эвристическим расстоянием h(x). Здесь в качестве h(x) хотелось бы иметь некоторую правдоподобную оценку истинного расстояния, для определения которой не надо находить кратчайший путь из x в цель. Например, для нашей задачи об оптимальном маршруте роль такого h(x), очевидно, могло бы выполнять "расстояние по прямой" в отличие от h(x), или истинного "расстояния по дороге".

Всем нам кажется оправданным, оказавшись на развилке незнакомой дороги, свернуть в направлении к цели. В равной мере разумным представляется и предложение Дорана и Мичи использовать для "стрижки" дерева решений не только принцип динамического программирования, но и эвристическую информацию и в связи с этим выращивать из каждой вершины только одну ветвь - ту, которая ведет к вершине с наименьшим эвристическим расстоянием до цели из числа ближайших соседей рассматриваемой вершины (рис. 54). Мы предлагаем читателю самому убедиться в том, что, приложив этот метод к плану на рис. 52, мы получим дерево решений, показанное на рис. 55, где подле каждой вершины в скобках указан этап, на котором она была получена. Для того чтобы иметь возможность проверять различные значения к, полезно иметь циркуль. Комментарии нужно читать в том порядке, в каком они перенумерованы.

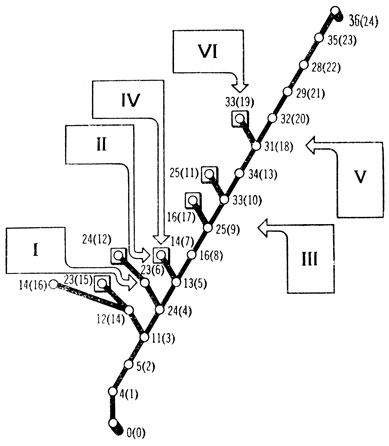
Рис. 55. На этой схеме есть только сплошные линии, соответствующие путям, которые действительно исследовались на окончательном варианте дерева. Цифры, стоящие у каждого узла, показывают: первая -номер узла на рис. 52, к которому ведет этот путь, а вторая (в скобках) -номер этапа, на котором был построен этот путь. Читателю придется пройти через 36 этапов для того, чтобы убедиться в справедливости примечаний к этапам 6, 7, 9, 7 (и снова ср. с 16, 18, 19). Почему включение этапа 11 ошибочно? I. 'Тупик': h (23)<h (16), хотя узел 16 'лучший' из соседей узла 13. II. Еще один 'тупик': h (14)<h (16). III. Здесь можно видеть основную слабость этого метода: от узла 25 'по прямой' очень близко до узла 36, но через разделяющую их пропасть нет Моста, а забравшись так далеко, не так-то просто 'отказаться' от уже проделанного планирования, вернуться назад, поближе к началу и пытаться строить совсем другой маршрут. IV. Этот путь будет 'закрыт' на этапе 16. V. Здесь пришлось затратить немало труда (с этапа 14 до 17) на исследование узлов, которые были 'ближе' к цели, прежде чем удалось продолжить движение к цели. VI. Алгоритм возвращает нас снова к узлу 33, но мы обрываем этот неэффективный путь, исходя из соображений динамического программирования

Упражнения. 1. Увеличьте вдвое протяженность прямого пути от пункта 11 к пункту 24 и постройте новое дерево решений. 2. Вместо "расстояния по воздуху" h{x) используйте "угловое отклонение" к\(х)} т. е. всегда выбирайте ту ветвь, которая возможно точнее направлена к цели. Какое дерево решения получится в этом случае?

Мы видим, что методом градиента найти путь к цели удалось всего за 26 шагов, несмотря на то что высота дерева равна 15, так что на каждый уровень приходится в среднем менее двух ветвей - это резко контрастирует с 14 ветвями, полученными для дерева на рис. 53, которое мы успели вырастить лишь до четвертого уровня.

Таким образом, при удачном выборе эвристического расстояния вроде использовавшегося в нашем примере число путей, которые нужно сравнивать, можно сократить до вполне приемлемого. Возможно, читатель уже заметил, что полученный предложенным методом маршрут не оптимален, а значит, сразу встает вопрос, существует ли такой способ использования эвристической информации, который позволял бы значительно сократить дерево решений и тем не менее давал бы оптимальное решение.

Положительный ответ на этот вопрос дали Харт, Нилссон и Рафаэл [105]. Суть их подхода иллюстрирует рис. 56: хотя здесь по-прежнему используется "расстояние по прямой", после узла "Начало пути" следует выбрать узел 1, а не узел 2, как в предыдущем методе; это связано с тем, что хотя узел 1 и дальше от цели, но зато он намного ближе к начальной точке.

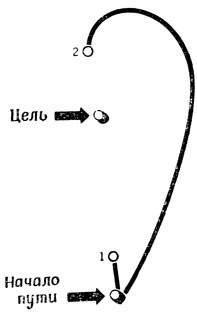
Рис. 56. Двигаться в узел 1 может оказаться разумнее потому, что хотя он дальше от цели, зато гораздо ближе к начальной точке

Выше мы видели, что Доран и Мичи построили свой алгоритм, пытаясь аппроксимировать поведение в случае, когда есть полная информация в виде функции h(x), т. е. протяженности кратчайшего пути из узла x в точку назначения. Наш новый алгоритм построен по тому же принципу, но только в нем используется другая форма представления полной информации, а именно функция f(x), определяющая протяженность кратчайшего пути из начала в точку назначения, который проходит через узел x. Понятно, что f(x) действительно несет полную информацию: из любого узла нужно двигаться в тот соседний узел, у которого f(x) имеет наименьшее значение, и полученный путь окажется оптимальным.

Пользуясь принципом динамического программирования, мы можем представить f(x) в виде суммы

f(x) = g(x)+h(x),

где h(x), как и раньше, - длина кратчайшего пути из x в цель, a g(x) - длина кратчайшего пути из начального состояния в x.

Как и прежде, мы можем аппроксимировать h(x) каким-то эвристическим расстоянием h(x), но чем можно аппроксимировать g(x)? Здесь мы примем подход, согласно которому в любой момент времени t, определяемого текущей фазой планирования, мы будем аппроксимировать g(x) с помощью g_t(x) - длины наикратчайшего пути в x из начального состояния среди тех путей, которые мы уже перебрали до момента времени t. Другими словами, мы аппроксимируем f(x) в момент времени t с помощью функции

f_t(x)=g_t(x)+h(x).

Харт, Нилссон и Дьюда предложили использовать эту эвристическую информацию для "сокращения" дерева решения (в дополнение к сокращению это связано с соображениями динамического программирования), отводя от каждого узла только ту ветвь, которая ведет к узлу с "минимальной эвристической длиной пути" f_t(x) среди всех ближайших соседей исходного узла. Они смогли доказать, что если h(x) никогда не бывает больше, чем h(x) [как в нашем случае, когда h(x) - это расстояние по прямой и, следовательно, не может быть больше h(x)], то этот алгоритм всегда дает оптимальное решение.

Читатель может убедиться, что этот метод заслуживает доверия, проверив, что представленный на рис. 57 результат его применения к задаче, поставленной на рис. 52, действительно совпадает с кратчайшим путем "с работы в гости". Интересно отметить также, что теперь поиск потребовал всего 23 шага и привел к оптимальному решению, тогда как на рис. 55 нам понадобилось 26 шагов, и было найдено лишь субоптимальное решение. Таково, по-видимому, вознаграждение за дополнительную работу, которую приходится делать, следя за значениями g_t(x) при появлении каждого нового узла x.

Между прочим, читателю следует обратить внимание на то, что условию h(x)≥h(x) удовлетворяет и случай отсутствия информации [h(x)=0; в этом случае метод практически возвращает нас к полному перебору (рис. 53)], и случай полной информации [h(x)=h(x); при этом решение задачи нашим методом можно получить сразу и никаких ветвлений на пути из начального состояния к цели не возникнет].

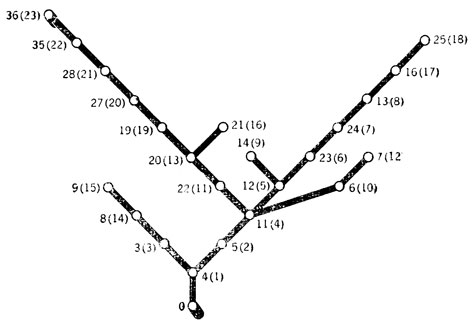
Рис. 57. Применение эвристики Харта, Нилссона и Рафаэла для задачи о кратчайшем маршруте на рис. 52. Метод построения этого дерева аналогичен приведенному на рис. 55, с той единственной разницей, что на каждом этапе строится не соседний узел, ближайший к цели, а соседний узел, для которого минимальна сумма 'пройденного расстояния, приводящего в этот узел из начала', и расстояния до цели 'по прямой'

Мы надеемся, что такое подробное изучение эвристического поиска в приложении к задаче об оптимальном маршруте убедило читателя, что многие процессы, на первый взгляд кажущиеся исключительно проявлением человеческого разума ("Ну, я посмотрел на рис. 52 и вижу два относительно прямых отрезка пути, один вначале, а другой в конце, ведут вроде бы навстречу друг другу, я их, знаете ли, соединил, и получился кратчайший путь"), можно представить в виде последовательности стандартных операций ("найти узел с наименьшим значением f_t(x)"), которые можно выполнять по заданной программе на вычислительной машине. Как должно было стать совершенно ясно из пяти предшествующих этому примеру замечаний, мы не собираемся утверждать, что именно эти операции происходят в мозгу человека; там наверняка происходят и другие процессы. Ранее, подчеркивая различия между исследованиями по искусственному интеллекту и теорий мозга, мы уже отмечали, что наша цель в этой главе состоит не в том, чтобы построить модель работы мозга, а в том, чтобы понять, как можно свести разумное поведение к последовательности элементарных операций в надежде (которая пока еще не оправдалась), что это поможет понять, каким образом активность нейронов позволяет нам вести себя разумным образом.

В заключение этого параграфа рассмотрим важную программу, послужившую одной из основ общего исследования эвристики, о которой мы только что говорили. Речь идет об "общем решателе задач" (ОРЗ) Ньюэлла, Шоу и Саймона [183]. Интересно, что их общая схема весьма близка к схеме Питса и Мак-Каллока (разд. 3.3), как показывают комментарии, данные в квадратных скобках. ОРЗ представляет собой общую схему решения задач следующего типа.

1. Имеется заданное множество объектов. [У Питтса и Мак-Каллока ему соответствует множество образцов.]

2. Задан конечный набор оценок различий и способ определения различий между двумя заданными объектами. [У Питтса и Мак-Каллока этому соответствует функция ошибки E, но, поскольку у ОРЗ набор различных оценок конечен, эти оценки дают лишь грубые указания на то, "чего нам недостает".]

3. Задан конечный набор операторов и таблица операторов - оценок различий, определяющая, при каком различии какой оператор вероятнее всего уменьшит это различие. [У Питтса и Мак-Каллока этому соответствует генератор преобразований.]

4. Задан исходный объект (например, список аксиом логики высказываний) и конечный объект (например, утверждение, истинность которого мы хотим доказать). Требуется найти последовательность операторов, которая преобразует исходный объект в требуемый (если операторам соответствуют правила логического вывода, то искомая последовательность операторов, даст требуемое доказательство искомого утверждения).

Вся хитрость здесь заключается в том, что, поскольку используемая шкала различий дает лишь очень незначительную информацию о том, что же нужно изменить, нет никакой гарантии, что использование оператора, рекомендованного в таблице, действительно преобразует имеющийся объект в другой, который будет ближе к цели. Более того, нет даже гарантии, что этот оператор вообще можно применить к имеющемуся объекту, и иногда приходится искать промежуточное преобразование, которое должно подготовить исходный объект к возможности применения "желаемого" оператора. В связи с этим уже нельзя действовать шаг за шагом, как в схеме Питтса - Мак-Каллока. Вместо этого приходится строить "дерево решений", регистрирующее, какие использовались операторы и на каких этапах. Цель занимающегося этим блока общего наблюдения программы ОРЗ состоит в том, чтобы обеспечить такое использование ресурсов, при котором максимально "росли" бы ветви дерева, по-видимому, ведущие к цели, как на рис. 58.

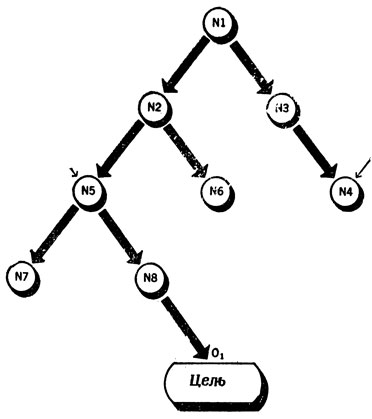
Рис. 58. Пример 'дерева решений', которое может быть построено блоком общего контроля программы ОРЗ. Различия между N5 и целью кажутся менее значительными, чем различия между целью и N6, и поэтому все внимание сосредоточивается на этом пути; N4 кажется даже дальше от цели, чем N1, и поэтому дальнейшего исследования этого пути не производится

В каждом узле мы можем определить различие между имеющимся объектом и целью, а затем выяснить, какой оператор рекомендует использовать в этом случае таблица. Может оказаться, что некоторые из них сразу применить нельзя. Исходя из всех этих соображений, мы должны решить, в какой узел следует двигаться дальше и какой из возможных операторов применять.

Таким образом, в ОРЗ предусмотрена функция наблюдения - управления с запоминанием различных участков пути, которые, как может выясниться в дальнейшем, может быть, и ведут к цели, и именно организация этой программы управления и отличает по-настоящему ОРЗ от схемы Питтса - Мак-Каллока.

Общий подход, характерный для ОРЗ, был использован Миллером, Галантером и Прибрамом [167] в качестве основы Для их программного подхода к психологии, изложенного в книге "Планы и структуры поведения". В этой книге под понятием план имеется в виду "некоторый иерархический процесс, позволяющий управлять порядком выполнения некоторой последовательности операций", и высказывается предположение, что такой план определяет механизм преобразования понимания в действие, до этого времени остававшийся вне рамок теории познания. Авторы этой книги предполагают также, что организму доступны многие другие планы помимо того, который действительно используется.

Основная с функциональной точки зрения часть их теории сродни таблице операций - различий программы ОРЗ или схемам, типа показанной на рис. 37. Блок ПВПВ (где ПВПВ означает Проверку, Выполнение, Проверку, Вывод), схема которого приведена на рис. 59, представляет собой систему с обратной связью, осуществляющую многократные проверки и пробные действия до тех пор, пока не будет достигнуто согласование между желаемым и планируемым положением вещей.

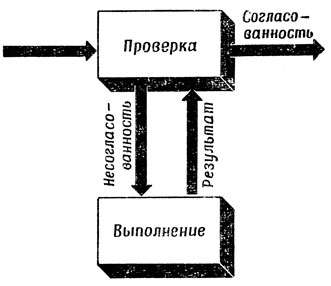
Рис. 59. Блок ПВПВ. Операция повторяется до тех пор, пока проверка не установит соответствия между имеющимся и требуемым

Миллер, Галантер и Прибрам [167] утверждают, что всякий план по своей форме - это иерархическая структура из блоков ПВПВ. Например, план забивания гвоздя можно описать так, как показано на рис. 60, где блок выполнения, входящий в блок ПВПВ для всей операции в целом, представлен в виде двух других блоков ПВПВ. Именно в этом и проявляется иерархическая структура плана. Теория требует использования дополнительных механизмов, которые предотвращают зацикливание, возникающее при бесконечных неудачных проверках (если, например, вы попали на сучок), и позволяют прерывать процесс (например, если вы попали молотком по пальцу). Отметим, что в нашем блоке ПВПВ все параметры состояния контура обрат ной связи можно наблюдать извне, тогда как в более сложных иерархических структурах многие состояния остаются внутренними и скрыты от наблюдения.

В какой области головного мозга разрабатываются подобные планы? Авторы приводят результаты физиологических исследований, которые, по их мнению, показывают, что план поведения выбирается или заменяется другим в лобной коре (которая, как мы должны считать, занята вопросами тактики), а за его реализацию отвечает лимбическая система. Люди после фронтальной лоботомии ведут себя так, как если бы за их "настоящим" не стояло будущего. И дело не в том, что им все равно; они, по-видимому, просто не в состоянии планировать свое поведение на будущее, как это делают "нормальные" люди.

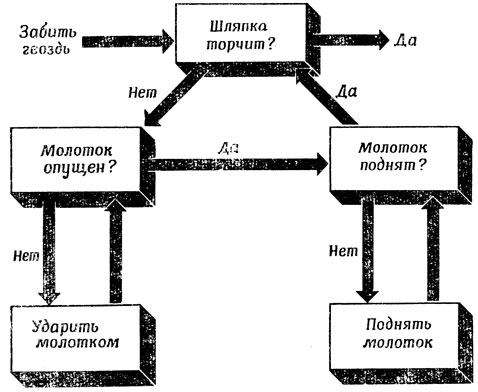
Рис. 60. Иерархический план, в котором блок выполнения глобальной системы ПВПВ представлен в виде двух систем ПВПВ более низкого уровня

Кроме того, у них несколько ослаблена мотивация - еще один симптом существования лишь ради сиюминутных целей. Можно считать, что в задачу выбора внутренней среды и, по крайней мере частично, во взаимодействие с ней вовлечен также и гипоталамус. Направленность внимания в значительной степени оценивается в таких понятиях, как "цель" или "намерение"; поэтому в любое время должно производиться определение ценностей или хотя бы важности того или иного факта. Такая система ценностей вырабатывается на основании опыта, наследственного или личного, и связана с выживанием. Последствия действий, оцененные по этим критериям как "благоприятные" или "неудачные", могут подкреплять или ослаблять будущие акты, в результате чего возникает иерархия выбора, закладываемая в центральную нервную систему. Но все это весьма умозрительно, и за годы, прошедшие до времени выхода этой книги, авторы изменили ряд своих физиологических интерпретаций.

Вместо того чтобы пытаться искать корреляцию между структурой ПВПВ и устройством различных областей мозга, гораздо интереснее разобраться в "расхождениях" между устройством ОРЗ и ПВПВ. Целью ОРЗ является, если ограничиться одним примером, напечатать правильное доказательство теоремы. Задача же соответствующей системы ПВПВ состоит в достижении такого состояния, когда никаких теорем доказывать не нужно. И в этом заключены глубокие различия между разными направлениями в теории человеческого поведения. Теории гомеостаза обращают главное внимание на поддержание постоянства основных параметров организма: содержание сахара и кислорода в крови, температуры тела и т. п., и объясняют человеческий интеллект как некий выкрутас, придуманный природой в процессе эволюции для того, чтобы решить эту проблему регулирования нескольких переменных. Другие люди, которым хотелось бы понять, как Бетховен мог создать свои симфонии, считают, что проблемы гомеостаза не имеют к этому никакого отношения. И быть может, примирить эти два подхода удастся после того, как, поняв, каким образом в процессе эволюции мозг научился решать проблемы выживания в столь невероятно многообразной среде, мы поймем и то, каким образом он строит такие разнообразные внутренние модели, что они могут охватить не только все трудности жизни в современном обществе, но также сферу фантазии и воображения.

В любом случае мы закончим на этом наш экскурс в область психологии и сделаем еще несколько замечаний об ОРЗ, которые позволят увидеть последние достижения "эвристического программирования" в более правильном свете.

Претензии ОРЗ на общность основаны на том, что эта программа может решить любую задачу, например доказать любую теорему исчисления высказываний, которая может быть решена с помощью поиска по дереву решений (типа приведенного на рис. 58) и таблицы операторов - оценок различий. К сожалению, именно эта общность подхода затрудняет использование в его рамках специальных приемов, придуманных для решения специальных задач. Кроме того, не все задачи можно решить таким способом, и, даже если такой подход возможен, мы видим настоящее проявление творческого интеллекта не столько в удачном применении таблицы операторов - оценок различий, сколько в осознании того, какие именно различия существенны для данной задачи, и в построении на базе опыта таблицы операторов, позволяющих устранять эти различия. Возможно, что методы, родственные методу Ура и Восслера [249], составивших машинную программу, которая сама генерирует детектор признаков для распознавания образов, развиваясь, достигнут в конце концов такого уровня, когда их можно будет положить в основу программы автоматического формирования таблицы операторов- оценок различий в дополнение к пакету программ управления ОРЗ. Однако подлинное "творчество" при решении задач состоит, по-видимому, в чем-то другом - в том, чтобы "увидеть проблему в истинном свете".

Для того чтобы вкратце рассказать о работе Ура и Восслера [249] по распознаванию образов, в которой программа сама вырабатывает детекторы признаков и оценивает их работу, рассмотрим образы, представленные на большом квадрате (или формальной "сетчатке"), разбитой на очень мелкие квадратики. Если предположить, что размеры такой сетчатки 20X20, то один из подходов к глобальному распознаванию образов может заключаться в том, чтобы рассматривать квадраты размерами, скажем, 5X5 в поисках признаков, которые могут помочь распознаванию. [В более сложном варианте эта процедура используется на ранних этапах предварительной обработки. Например, полезные признаки можно искать по кусочно-линейному представлению образа (ср. с рассмотрением зрительной системы кошки в разд. 2.4).] Так, при распознавании букв латинского алфавита полезными признаками служат: маленькая перевернутая буква V, образующая верхнюю часть буквы А, наклонная линия ее ножки, полукружья в букве В и т. п. Программа Ура и Восслера генерировала подобные эталоны размером 5X5 случайным образом и затем опробовала их на большом числе различных букв, предъявляемых на стадии обучения. Сущность их подхода состоит в том, чтобы независимо от уровня, на котором генерируются эти эталоны, отбирать те из них, которые оказались тесно связанными с одними буквами и совсем не подходят для других и, значит, полезны при дискриминации. Те же эталоны, которые не связаны определенно ни с какими буквами, отбрасываются, и в конце концов в машине оказывается список признаков, позволяющий очень хорошо различать разные буквы алфавита.

Приведем теперь два примера того, насколько важную роль играет для человека, решающего какую-то задачу, способность представить ее в такой форме, которая открывает более простой путь к решению. Для начала рассмотрим игру, в которой два лица по очереди называют любые целые числа от 1 до 9 при условии, что это число не было названо ранее, а выигрывает тот, кто первый сможет дополнить сумму названных до этого чисел до пятнадцати. Для некоторых это трудная игра, пока они не поймут, что с помощью магического квадрата (рис. 61) эту игру можно свести к игре в крестики-нолики.

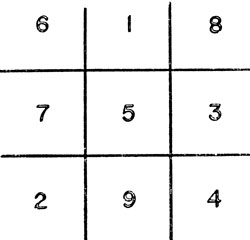
Рис. 61. Магический квадрат и игра в крестики-нолики

Сумма цифр во всех строках и столбцах этого квадрата, а также на его главных диагоналях равна 15.

Рассмотрим затем следующую задачу (рис. 62). Покрыть фигуру, получившуюся из квадрата со стороной в 8 единиц с вырезанными из двух противоположных углов квадратиками размером 1X1 прямоугольниками размером 2X1. Оказывается, что сделать этого нельзя. Но как это доказать?! Не с помощью же перебора всех возможных способов покрытия? На самом деле эту задачу можно решить методом математической индукции по размерам большого квадрата, но доказать это гораздо проще, воспользовавшись удобным представлением исходной задачи. Для этого представим себе, что исходный большой квадрат - это шахматная доска. Нетрудно убедиться в том, что каждый прямоугольник 2X1 покрывает одно черное и одно белое поле этой доски при любом способе покрытия. А это значит, что число покрытых белых и черных полей при любом покрытии должно быть одинаковым, чего не может быть в данном случае, поскольку из нашей шахматной доски вырезаны два поля одинакового цвета.

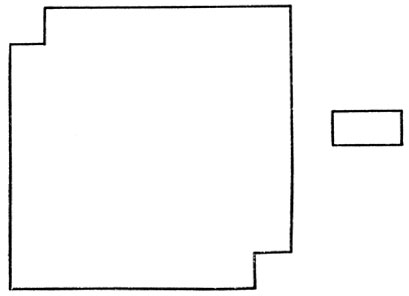
Рис. 62. Можно ли покрыть прямоугольниками размером 1X2 фигуру, полученную из квадрата 8X8, у которой из двух противоположных углов вырезали по квадратику 1X1

Конечно, все это никак не помогает решить вопрос об источнике удачной формы представления. И нам остается только, добавив к нашему списку "ингредиентов" интеллекта высокого уровня "способность находить удачные представления", перейти к следующему разделу, где мы узнаем, как вычислительная машина может анализировать изображение своей среды на телевизионном экране, пользуясь тем, что перечень различных объектов, с которыми ей, возможно, придется иметь дело, ей заранее известен.